题目内容
已知以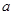 为首项的数列
为首项的数列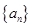 满足:
满足: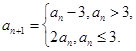
(1)若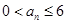 ,求证:
,求证: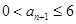 ;
;
(2)若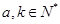 ,求使
,求使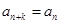 对任意正整数n都成立的
对任意正整数n都成立的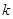 与
与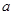 .
.
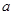 为首项的数列
为首项的数列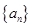 满足:
满足: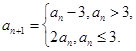
(1)若
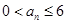 ,求证:
,求证: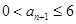 ;
; (2)若
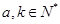 ,求使
,求使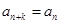 对任意正整数n都成立的
对任意正整数n都成立的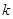 与
与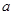 .
.(1)证明过程详见解析;(2)当 时,满足题意的
时,满足题意的 N*; 当
N*; 当 时,满足题意的
时,满足题意的 N*.
N*.
 时,满足题意的
时,满足题意的 N*; 当
N*; 当 时,满足题意的
时,满足题意的 N*.
N*.试题分析:本题考查数列与函数的综合知识.第一问,将
 从3断开,分成两部分,分别求出
从3断开,分成两部分,分别求出 的范围;第二问,分别验证每一种情况.
的范围;第二问,分别验证每一种情况.试题解析:(1)当
 时,则
时,则
 ,当
,当 时,则
时,则 ,
,故
 ,所以当
,所以当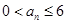 时,总有
时,总有 . 8分
. 8分(2)①当
 时,
时, ,故满足题意的
,故满足题意的 .
.同理可得,当
 或4时,满足题意的
或4时,满足题意的 N*.
N*.当
 或6时,满足题意的
或6时,满足题意的 N*.
N*. ②当
 时,
时, ,故满足题意的k不存在.
,故满足题意的k不存在. ③当
 时,由(1)知,满足题意的k不存在.
时,由(1)知,满足题意的k不存在. 综上得:当
 时,满足题意的
时,满足题意的 N*;
N*; 当
 时,满足题意的
时,满足题意的 N*. 16分.
N*. 16分.
练习册系列答案
相关题目
 则f(3)=________.
则f(3)=________. 有三个不同的零点,则实数
有三个不同的零点,则实数 的取值范围是_____.
的取值范围是_____. ,函数
,函数 ,若
,若 ,则
,则 的值为 .
的值为 . ,定义函数
,定义函数 给出下列命题:
给出下列命题: ; ②函数
; ②函数 是奇函数;③当
是奇函数;③当 时,若
时,若 ,
, ,总有
,总有 成立,其中所有正确命题的序号是( )
成立,其中所有正确命题的序号是( )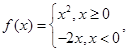 则关于x的方程
则关于x的方程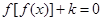 的根的情况,有下列说法:
的根的情况,有下列说法: 上的函数
上的函数 ,则
,则 ( )
( )

 对定义域
对定义域 内的任意
内的任意 都有
都有 ,且当
,且当 时其导函数
时其导函数 满足
满足 若
若 则( )
则( )



 则
则 ( )
( )


