题目内容
已知函数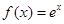
，
，
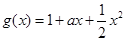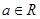
（I）设函数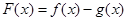
，讨论
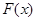的极值点的个数；
（II）若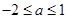
，求证：对任意的
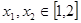，且
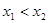时，都有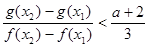
【答案】
（I）
的极值点个数为
个；（II）见解析.
【解析】
（1）讨论的极值点的个数，需求
；然后令导数为0，讨论零点左右的导数值的正负；
（2）整理 
转化为讨论
在
上单调性，再次利用导数判断。
解：（I）
，，
，
，得
当
时，
，从而
在
上单调递减，当
时，
，从而在上单调递增，所以
，
当
，即
时，
恒成立，的极值点个数为
；
当
，即
时，（又
）
的极值点个数为个
（II）证明：
在上单调递增
在
上恒成立
令
，关于
是一次函数。
又
，
，(由
得)
所以
在上恒成立，所以，原命题成立。
练习册系列答案
教学练新同步练习系列答案
相关题目
求：
的图象关于点
中心对称，并求
的值；
，且1＜a1＜2，求证
+…+
＜2.
，
．
时，
在
上是增函数；
，试说明存在实数
，当
时，
．
，
．
是函数
图象的一条对称轴，求
的值．
的单调递增区间．
，
．
，
。
的单调区间；
，曲线C与其在点
处的切线交于另一点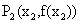
，曲线C与其在点
，线段
（Ⅰ）（ii）的正确命题，并予以证明。