题目内容
20.已知定义在正实数集上的函数f(x)=
x2+2ax，g(x)=3a2lnx+b，其中a＞0.设两曲线y=f(x)，y=g(x)有公共点，且在该点处的切线相同.（Ⅰ）用a表示b，并求b的最大值；
（Ⅱ）求证：f(x) ≥g(x) (x＞0).
本小题主要考查函数，不等式和导数的应用等知识，考查综合运用数学知识解决问题的能力。
解：（Ⅰ）设y=f(x)与y=g(x)(x＞0)在公共点(x0,y0)处的切线相同。
，
，由题意f(x0)=g(x0),f′(x0)=g′(x0).
即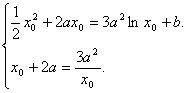
由
得：x0=a,或x0=-3a(舍去)。
即有
令
，则
.于是
当t(1-3lnt)＞0,即
时，h′(t)＞0;
当t(1-3lnt)＜0,即
时，h′(t)＜0.
故h(t)在
为增函数，在
为减函数。
于是h(t)在
的最大值为
。
（Ⅱ）设F(x)=f(x)-g(x)=
x2+2ax-3a2lnx-b(x＞0).
则
。
故F(x)在(0,a)为减函数，在
为增函数。
于是函数F(x)在
上的最小值是F(a)=F(x0)=f(x0)-g(x0)=0.
故当x＞0时，有f(x)-g(x)≥0，即当x＞0时，f(x)≥g(x).
练习册系列答案
相关题目