题目内容
如果函数f（x）=cos（2x+φ）的图象关于点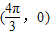
成中心对称，且
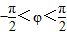，则函数
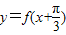为（ ）A．奇函数且在
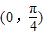上单调递增B．偶函数且在
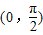上单调递增C．偶函数且在
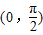上单调递减D．奇函数且在
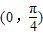上单调递减
【答案】分析：2×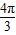
+∅=kπ+
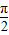，k∈z，再由 
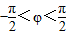，可得∅=-
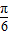，从而求得函数f（x）的解析式，从而得到f（x+3）的解析式．
解答：解：函数f（x）=cos（2x+φ）的图象关于点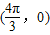
成中心对称，
∴2×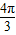
+∅=kπ+
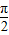，k∈z．
再由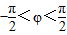
，可得∅=-
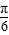，故函数f（x）=cos（2x-
），
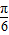故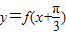
=cos[2（x+
）-
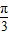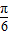]=cos（2x+
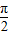）=-sin2x，
故函数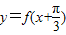
为奇函数且在
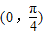上单调递减，
故选D．
点评：本题主要考查由函数y=Asin（ωx+∅）的部分图象求函数的解析式，余弦函数的对称性，属于中档题．
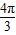+∅=kπ+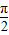，k∈z，再由 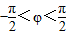，可得∅=-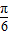，从而求得函数f（x）的解析式，从而得到f（x+3）的解析式．解答：解：函数f（x）=cos（2x+φ）的图象关于点
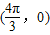成中心对称，∴2×
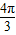+∅=kπ+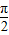，k∈z．再由
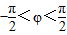，可得∅=-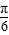，故函数f（x）=cos（2x-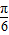），故
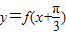=cos[2（x+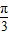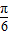）-]=cos（2x+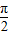）=-sin2x，故函数
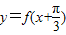为奇函数且在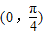上单调递减，故选D．
点评：本题主要考查由函数y=Asin（ωx+∅）的部分图象求函数的解析式，余弦函数的对称性，属于中档题．
练习册系列答案
相关题目
如果函数f（x）=|lg|2x-1||在定义域的某个子区间（k-1，k+1）上不存在反函数，则k的取值范围是（ ）
A、[-
| ||||
B、(1，
| ||||
| C、[-1，2） | ||||
D、(-1，-
|