题目内容
已知函数 (a>0,c∈R)为奇函数,当x>0时,f(x)的最小值为2.
(a>0,c∈R)为奇函数,当x>0时,f(x)的最小值为2.
(I)求函数的解析式
(Ⅱ)若a+b=1,a、b∈R+,求证:
(Ⅲ) 若g(x)=f(x)-x,n∈N*且n≥2,求证: .
.
解:(I)由函数 (a>0,c∈R)为奇函数,
(a>0,c∈R)为奇函数,
可得f(-x)= =-f(x)=-
=-f(x)=-
∴-x+c=-x-c
∴c=0
∴
再由x>0时, ≥
≥ ,
,
∵f(x)的最小值为2,得2 =2,?a=1,
=2,?a=1,
故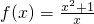 (x≠0)…(4分)
(x≠0)…(4分)
(Ⅱ)欲证原不等式成立,
需证: .
.
因为 a+b=1,即证: ,
,
再由a+b=1,a、b∈R+, ,故
,故 ,
,
令t=ab,考察函数y=t+ ,它在区间(0,
,它在区间(0, ]上是单调减函数,当t=
]上是单调减函数,当t= 时,y=
时,y=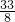 ,
,
∴ ,
,
从而原不等式成立.…(8分)
(学生用其它方法参照给分)
(Ⅲ)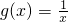 ,需证:
,需证:
一方面:

…(10分)
另一方面:


综上 .
.
…(14分)
分析:(I)先根据函数为奇函数即f(-x)=-f(x)求得c=0,进而根据均值不等式求得函数f(x)的最小值的表达式,结果为2求得a,进而求得函数f(x)的解析式;
(II)利用分析法进行证明.欲证原不等式成立,只需证: .因为 a+b=1,即证:
.因为 a+b=1,即证: ,令t=ab,考察函数y=t+
,令t=ab,考察函数y=t+ ,结合此函数在区间(0,
,结合此函数在区间(0, ]上是单调减函数即得;
]上是单调减函数即得;
(III)用分析法证明.分析得出只需证: ,下面从而左右两个方面进行证明即可.
,下面从而左右两个方面进行证明即可.
点评:本题主要考查了函数的奇偶性的应用,均值不等式的应用,不等式的证明及函数的单调性.考查了学生综合分析问题和解决问题的能力.
 (a>0,c∈R)为奇函数,
(a>0,c∈R)为奇函数,可得f(-x)=
 =-f(x)=-
=-f(x)=-
∴-x+c=-x-c
∴c=0
∴

再由x>0时,
 ≥
≥ ,
,∵f(x)的最小值为2,得2
 =2,?a=1,
=2,?a=1,故
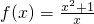 (x≠0)…(4分)
(x≠0)…(4分)(Ⅱ)欲证原不等式成立,
需证:
 .
.因为 a+b=1,即证:
 ,
,再由a+b=1,a、b∈R+,
 ,故
,故 ,
,令t=ab,考察函数y=t+
 ,它在区间(0,
,它在区间(0, ]上是单调减函数,当t=
]上是单调减函数,当t= 时,y=
时,y=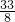 ,
,∴
 ,
,从而原不等式成立.…(8分)
(学生用其它方法参照给分)
(Ⅲ)
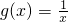 ,需证:
,需证:
一方面:

…(10分)
另一方面:



综上
 .
.…(14分)
分析:(I)先根据函数为奇函数即f(-x)=-f(x)求得c=0,进而根据均值不等式求得函数f(x)的最小值的表达式,结果为2求得a,进而求得函数f(x)的解析式;
(II)利用分析法进行证明.欲证原不等式成立,只需证:
 .因为 a+b=1,即证:
.因为 a+b=1,即证: ,令t=ab,考察函数y=t+
,令t=ab,考察函数y=t+ ,结合此函数在区间(0,
,结合此函数在区间(0, ]上是单调减函数即得;
]上是单调减函数即得;(III)用分析法证明.分析得出只需证:
 ,下面从而左右两个方面进行证明即可.
,下面从而左右两个方面进行证明即可.点评:本题主要考查了函数的奇偶性的应用,均值不等式的应用,不等式的证明及函数的单调性.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
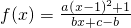 (a,b,c∈N),且f(2)=2,f(3)<3,
(a,b,c∈N),且f(2)=2,f(3)<3,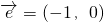 平移后得到的图象关于原点对称.
平移后得到的图象关于原点对称. ,
, (a>0),若
(a>0),若 ,
, ,使得f(x1)= g(x2),则实数a的取值范围是( )
,使得f(x1)= g(x2),则实数a的取值范围是( ) (B)
(B)
 (C)
(C)
 (D)
(D)

 (a,b,c∈N),且f(2)=2,f(3)<3,
(a,b,c∈N),且f(2)=2,f(3)<3, 平移后得到的图象关于原点对称.
平移后得到的图象关于原点对称. (A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且
(A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且 ,则函数y=f(x)在
,则函数y=f(x)在 上的最小值是( )
上的最小值是( )

