题目内容
已知双曲线与椭圆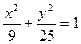
共焦点，它们的离心率之和为
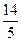，求双曲线方程.(10分)
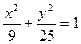共焦点，它们的离心率之和为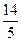，求双曲线方程.(10分) 双曲线方程为: 
由于椭圆焦点为F(0,
4),离心率为e=
,所以双曲线的焦点为F(0,4),离心率为2,
从而c=4,a=2,b=2
.
所以求双曲线方程为:
4),离心率为e=,所以双曲线的焦点为F(0,4),离心率为2,从而c=4,a=2,b=2
.所以求双曲线方程为:
练习册系列答案
相关题目
题目内容
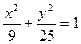共焦点，它们的离心率之和为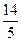，求双曲线方程.(10分) 4),离心率为e=,所以双曲线的焦点为F(0,4),离心率为2,.
是双曲线
上一点，且满足
，则该点
一定位于双曲线（ ）
=1有共同的焦点,且与此椭圆一个交点的纵坐标为4,求这个双曲线的方程.
，该动点的轨迹为F，
的最小值。