题目内容
已知平面向量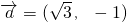
，
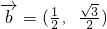
（1）证明：
；
（2）若存在实数k和t，满足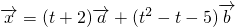
，
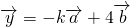，且
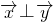，试求出k关于t的关系式，即k=f（t）；
（3）根据（2）的结论，试求出函数k=f（t）在t∈（-2，2）上的最小值．
解：（1）∵
，
∴；
（2）由（1）可知
，且
，
∴
，
∴
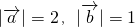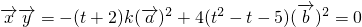（t≠-2）；
（3）
，
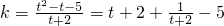∵t∈（-2，2），
∴t+2＞0，
则
，
当且仅当t+2=1，
，即t=-1时取等号，
∴k的最小值为-3．
分析：（1）根据题意，证其数量积为0即可，
（2）有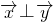 得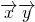
=0再用（1）的结论整理即得，
（3）利用基本不等式a+b≥2
求最值，或利用导数求出最小值
点评：本题考查向量的数量积判断两个向量的垂直关系，及利用基本不等式求最值的应用，考查计算能力，是基础题．
，∴
；（2）由（1）可知
，且，∴
，∴
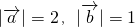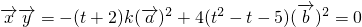（t≠-2）；（3）
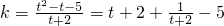，∵t∈（-2，2），
∴t+2＞0，
则
，当且仅当t+2=1，
，即t=-1时取等号，
∴k的最小值为-3．
分析：（1）根据题意，证其数量积为0即可，
（2）有
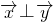得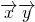=0再用（1）的结论整理即得，（3）利用基本不等式a+b≥2
求最值，或利用导数求出最小值点评：本题考查向量的数量积判断两个向量的垂直关系，及利用基本不等式求最值的应用，考查计算能力，是基础题．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
已知平面向量
=（1，2），
=（-2，m），且
∥
，则m的值为（ ）
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、4 | D、-4 |
已知平面向量
=（1，2），
=（-2，m），且
∥
，则|
|=（ ）
| a |
| b |
| a |
| b |
| b |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
已知平面向量
=（1，-2），
=（2，1），
=（-4，-2），则下列结论中错误的是（ ）
| a |
| b |
| c |
A、向量
| ||||||||
B、若
| ||||||||
C、对同一平面内任意向量
| ||||||||
D、向量
|