题目内容
18. 已知函数f(x)=$\left\{\begin{array}{l}{x^2}+2x,\;\;\;x<0\\ 0,\;\;\;\;\;\;\;\;\;\;\;x=0\\-{x^2}+2x,\;x>0\end{array}$.
已知函数f(x)=$\left\{\begin{array}{l}{x^2}+2x,\;\;\;x<0\\ 0,\;\;\;\;\;\;\;\;\;\;\;x=0\\-{x^2}+2x,\;x>0\end{array}$.(1)在所给的坐标系中画出该函数的图象;
(2)由图象写出的单调区间,并指出函数f(x)在区间[-2,2]上的最大值和最小值;
(3)若函数f(x)在区间[-1,a-2]上单调递增,求实数a的取值范围.
分析 (1)根据已知中函数的解析式,结合二次函数的图象和性质,可得函数图象;
(2)结合已知中函数的图象,可得函数的单调区间及区间[-2,2]上的最大值和最小值;
(3)若函数f(x)在区间[-1,a-2]上单调递增,则-1<a-2≤1,解得答案.
解答 解:(1)函数f(x)=$\left\{\begin{array}{l}{x^2}+2x,\;\;\;x<0\\ 0,\;\;\;\;\;\;\;\;\;\;\;x=0\\-{x^2}+2x,\;x>0\end{array}$的图象如下图所示: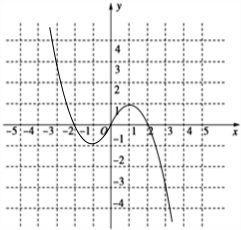
(2)由图可得:
函数f(x)的单调递增区间为:(-1,1);
函数f(x)的单调递减区间:(-∞,-1),(1,+∞);
在区间[-2,2]上,
函数f(x)的最大值1,
函数f(x)的最小值-1
(3)若函数f(x)在区间[-1,a-2]上单调递增,
则-1<a-2≤1,
解得:1<a≤3.
点评 本题考查的知识点是分段函数的应用,数形结合思想,函数的单调性和最值.

练习册系列答案
相关题目
9.数列{an}中,${a_1}=\frac{1}{2},{a_n}=\frac{1}{{1-{a_{n-1}}}}(n≥2,n∈N*)$,则a2015=( )
| A. | 2 | B. | -1 | C. | 1 | D. | $\frac{1}{2}$ |