题目内容
截止到1999年底,我国人口约13亿.如果今后能将人口平均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:设过x年后,我国人口为16亿,列出方程13×(1+1%)x=16,求出x的值即可.
解答:
解:设经过x年后,我国人口为16亿,
∴13×(1+1%)x=16,
即1.01x=
;
两边取常用对数得
lg1.01x=lg
,
则xlg1.01=lg16-lg13,
∴x=
=
=
≈20.95≈21;
答:经过21年后,我国人口为16亿.
∴13×(1+1%)x=16,
即1.01x=
| 16 |
| 13 |
两边取常用对数得
lg1.01x=lg
| 16 |
| 13 |
则xlg1.01=lg16-lg13,
∴x=
| lg16-1g13 |
| lg1.01 |
| 4×0.3010-1.1139 |
| 0.0043 |
| 901 |
| 43 |
答:经过21年后,我国人口为16亿.
点评:本题考查了增长率的问题,即考查了指数模型的应用问题,是基础题目.

练习册系列答案
相关题目
等比数列{an}中,首项a1=2,公比为3,Sn为其前n项和,则S4+a3等于( )
| A、44 | B、64 | C、98 | D、134 |
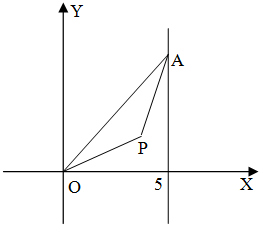 如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按逆时针方向排列),求点P的轨迹方程.
如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按逆时针方向排列),求点P的轨迹方程.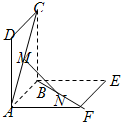 如图,已知四边形ABCD,ABEF都是矩形,M、N分别是对角线AC和BF的中点,则MN与平面BCE的关系是
如图,已知四边形ABCD,ABEF都是矩形,M、N分别是对角线AC和BF的中点,则MN与平面BCE的关系是