题目内容
已知
，且
，则
的最小值是
，且，则的最小值是| A．2 | B． | C． | D．8 |
C
令ab=t，由基本不等式可得 t∈（0，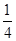
]，则=
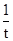+t，根据函数 y=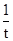+t 在（0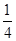，]上是减函数，可得当t= 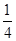时，函数 y 取得最小值 ，从而得到答案．
解答：解：a＞0，b＞0，且a+b=1，
令ab=t，则 由 1=（a+b）2=a2+b2+2ab≥4ab，
可得 0＜ab≤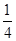，则 =
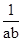+ab=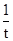+t，t∈（0，]．
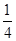由于函数 y=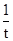+t 在（0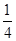，]上单调递减，故当 t= 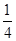时，函数 y 取得最小值 ，
故选C．
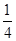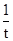]，则=+t，根据函数 y=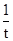+t 在（0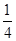，]上是减函数，可得当t= 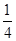时，函数 y 取得最小值 ，从而得到答案．解答：解：a＞0，b＞0，且a+b=1，
令ab=t，则 由 1=（a+b）2=a2+b2+2ab≥4ab，
可得 0＜ab≤
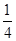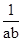，则 =+ab=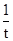+t，t∈（0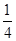，]．由于函数 y=
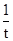+t 在（0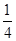，]上单调递减，故当 t= 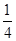时，函数 y 取得最小值 ，故选C．
练习册系列答案
阅读快车系列答案
相关题目
,则
的最小值是( )
的可导函数
满足
且
，则
的解集为
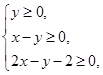则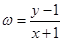
的取值范围是 。
，则按所做的第①题给分。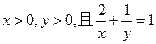
，若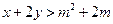
恒成立，则实数
的取值范围是 。
，
，且
，则
的最小值是 （ ）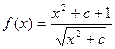 
的最小值是2，则实数
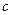的取值范围是
满足
，则
的最大值为 ．
，
，求
的范围。