题目内容
【题目】如图,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其左焦点到点P(2,1)的距离为
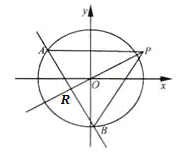
,其左焦点到点P(2,1)的距离为![]() .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
(Ⅰ)求椭圆C的方程;
(Ⅱ) 求![]() ABP的面积取最大时直线l的方程.
ABP的面积取最大时直线l的方程.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】(Ⅰ)由题:![]() ; (1)
; (1)
左焦点(﹣c,0)到点P(2,1)的距离为:![]()
![]() . (2)
. (2)
由(1) (2)可解得:![]() .∴所求椭圆C的方程为:
.∴所求椭圆C的方程为:![]() .
.
(Ⅱ)易得直线OP的方程:y=![]() x,设A(xA,yA),B(xB,yB),R(x0,y0).其中y0=
x,设A(xA,yA),B(xB,yB),R(x0,y0).其中y0=![]() x0.
x0.
∵A,B在椭圆上,
∴ .
.
设直线AB的方程为l:y=﹣![]() (m≠0),
(m≠0),
代入椭圆: .
.
显然![]() .
.
∴﹣![]() <m<
<m<![]() 且m≠0.
且m≠0.
由上又有:![]() =m,
=m,![]() =
=![]() .
.
∴|AB|=![]() |
|![]() |=
|=![]()
![]() =
=![]()
![]() .
.
∵点P(2,1)到直线l的距离为:![]() .
.
∴S![]() ABP=
ABP=![]() d|AB|=
d|AB|=![]()
![]() ,其中﹣
,其中﹣![]() <m<
<m<![]() 且m≠0.
且m≠0.
利用导数解:令![]() ,
,
则![]()
当m=![]() 时,有(S
时,有(S![]() ABP)max.
ABP)max.
此时直线l的方程![]()

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
