题目内容
如图,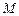 ,
,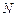 分别为锐角三角形
分别为锐角三角形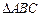 (
(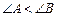 )的外接圆
)的外接圆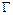 上弧
上弧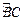 、
、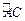 的中点.过点
的中点.过点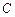 作
作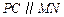 交圆
交圆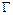 于
于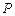 点,
点,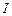 为
为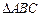 的内心,连接
的内心,连接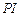 并延长交圆
并延长交圆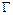 于
于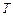 .
.
⑴求证: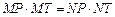 ;
;
⑵在弧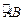 (不含点
(不含点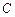 )上任取一点
)上任取一点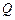 (
(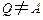 ,
,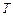 ,
,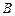 ),记
),记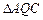 ,
,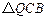 的内心分别为
的内心分别为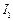 ,
,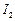 ,
,

求证: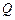 ,
,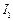 ,
,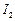 ,
,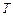 四点共圆.
四点共圆.
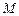 ,
,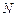 分别为锐角三角形
分别为锐角三角形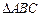 (
(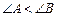 )的外接圆
)的外接圆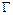 上弧
上弧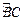 、
、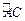 的中点.过点
的中点.过点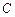 作
作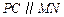 交圆
交圆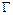 于
于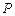 点,
点,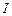 为
为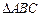 的内心,连接
的内心,连接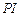 并延长交圆
并延长交圆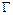 于
于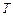 .
.⑴求证:
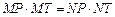 ;
;⑵在弧
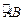 (不含点
(不含点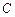 )上任取一点
)上任取一点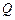 (
(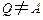 ,
,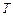 ,
,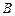 ),记
),记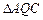 ,
,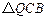 的内心分别为
的内心分别为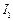 ,
,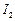 ,
,
求证:
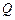 ,
,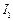 ,
,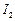 ,
,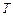 四点共圆.
四点共圆.⑴连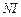 ,
,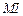 .由于
.由于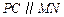 ,
,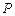 ,
,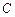 ,
,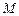 ,
,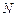 共圆,故
共圆,故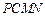 是等腰梯形.因此
是等腰梯形.因此 ,
,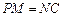 .
.
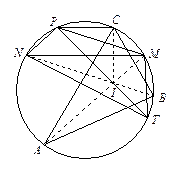
连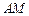 ,
,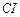 ,则
,则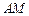 与
与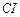 交于
交于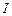 ,因为
,因为
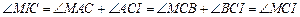 ,
,
所以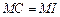 .同理
.同理
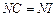 .
.
于是
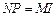 ,
,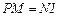 .
.
故四边形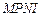 为平行四边形.因此
为平行四边形.因此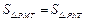 (同底,等高).
(同底,等高).
又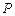 ,
,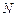 ,
,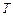 ,
,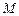 四点共圆,故
四点共圆,故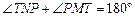 ,由三角形面积公式
,由三角形面积公式
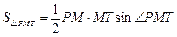
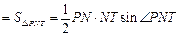
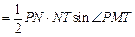
于是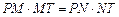 .
.
⑵因为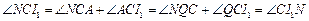 ,
,

所以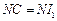 ,同理
,同理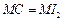 .由
.由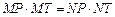 得
得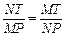 .
.
由⑴所证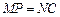 ,
, ,故
,故
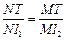 .
.
又因
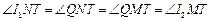 ,
,
有
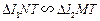 .
.
故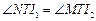 ,从而
,从而
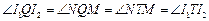 .
.
因此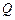 ,
,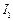 ,
,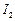 ,
,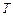 四点共圆.
四点共圆.
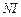 ,
,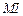 .由于
.由于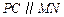 ,
,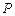 ,
,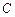 ,
,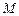 ,
,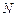 共圆,故
共圆,故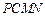 是等腰梯形.因此
是等腰梯形.因此 ,
,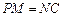 .
.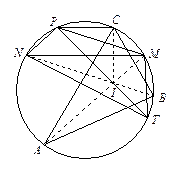
连
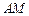 ,
,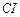 ,则
,则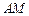 与
与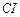 交于
交于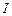 ,因为
,因为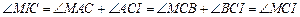 ,
,所以
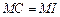 .同理
.同理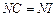 .
.于是
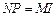 ,
,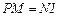 .
.故四边形
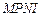 为平行四边形.因此
为平行四边形.因此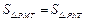 (同底,等高).
(同底,等高).又
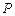 ,
,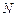 ,
,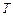 ,
,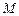 四点共圆,故
四点共圆,故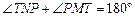 ,由三角形面积公式
,由三角形面积公式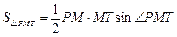
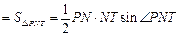
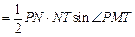
于是
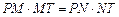 .
.⑵因为
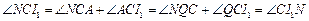 ,
,
所以
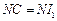 ,同理
,同理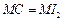 .由
.由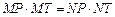 得
得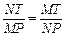 .
.由⑴所证
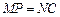 ,
, ,故
,故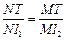 .
.又因
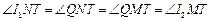 ,
,有
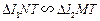 .
.故
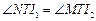 ,从而
,从而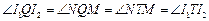 .
.因此
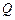 ,
,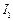 ,
,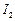 ,
,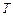 四点共圆.
四点共圆.
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
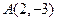 和
和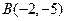 ,且圆心C在直线
,且圆心C在直线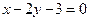 上,求圆C的方程.
上,求圆C的方程.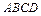 中,
中,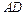 ∥BC,点
∥BC,点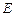 ,
,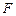 分别在边
分别在边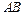 ,
,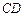 上,设
上,设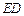 与
与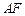 相交于点
相交于点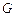 ,若
,若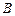 ,
,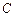 ,
,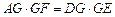 .
. 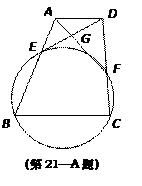
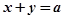 与圆
与圆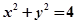 交于A、B两点,且
交于A、B两点,且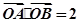 (其中O为原点),则实数a等于
(其中O为原点),则实数a等于 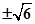 B、
B、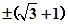 C、
C、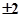 D、
D、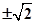
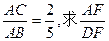 的值.
的值.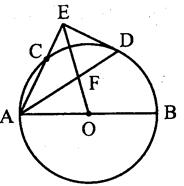
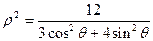 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为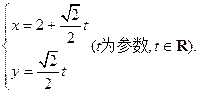
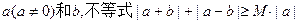 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。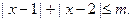
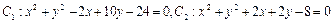 ,则以两圆公共弦为直径的圆的方程是 .
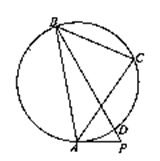
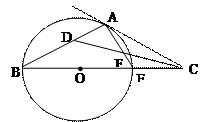
,则以两圆公共弦为直径的圆的方程是 . 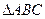 是圆的内接三角形,PA切圆于点A,PB交圆于点D。若
是圆的内接三角形,PA切圆于点A,PB交圆于点D。若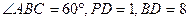 ,则
,则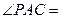 ,PA= 。
,PA= 。