题目内容
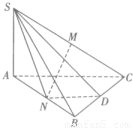
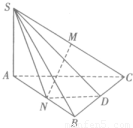
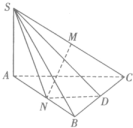 如图,△ABC是以∠ABC为直角三角形,SA⊥平面ABCD,SA=BC=2,AB=4.M、N、D分别是SC、AB、BC的中点.
如图,△ABC是以∠ABC为直角三角形,SA⊥平面ABCD,SA=BC=2,AB=4.M、N、D分别是SC、AB、BC的中点.(1)求证:MN⊥AB;
(2)(文科)求二面角S-ND-A的余弦值;
(3)(理科)求点A到平面SND的距离.
分析:(1)取AC的中点E,连接ME,NE,根据SA⊥平面ABCD,根据线面垂直的第二判定定理可得ME⊥平面ABC,则NE为MN在平面ABC内的射影,由NE⊥AB,结合由三垂线定理可得MN⊥AB;
(2)过A作AF⊥DN与DN的延长线相交于点F,连接SF,由三垂线定理知,∠SFA即为二面角S-ND-A的平面角,解三角形,即可得到二面角S-ND-A的余弦值;
(3)过点A作AH⊥SF于H,结合(2)的结论,易得AH的长即为点A到平面SND的距离,解Rt△AHF,即可求出点A到平面SND的距离.
(2)过A作AF⊥DN与DN的延长线相交于点F,连接SF,由三垂线定理知,∠SFA即为二面角S-ND-A的平面角,解三角形,即可得到二面角S-ND-A的余弦值;
(3)过点A作AH⊥SF于H,结合(2)的结论,易得AH的长即为点A到平面SND的距离,解Rt△AHF,即可求出点A到平面SND的距离.
解答: 证明:(1)取AC的中点E,连接ME,NE,则ME∥SA
证明:(1)取AC的中点E,连接ME,NE,则ME∥SA
又∵SA⊥平面ABC,
∴ME⊥平面ABC
∴NE为MN在平面ABC内的射影
又∵N,E分别为AB,AC的中点
∴NE∥BC
∴NE⊥AB
由三垂线定理知MN⊥AB
(2)过A作AF⊥DN与DN的延长线相交于点F,连接SF
由三垂线定理知,∠SFA即为二面角S-ND-A的平面角
在Rt△DBN中,tan∠DNB=
=
∴sin∠DNB=
在Rt△AFN中,NF=AN•sin∠DNB=
在Rt△SAF中,tan∠SFA=
=
∴cos∠SFA=
即二面角S-ND-A的余弦值为
(3)过点A作AH⊥SF于H
由(2)知平面SAF⊥平面SND
∴AH⊥平面SND
∴AH的长即为点A到平面SND的距离
在Rt△AHF中,AH=AF•sin∠SAF=
•
=
故点A到平面SND的距离为
 证明:(1)取AC的中点E,连接ME,NE,则ME∥SA
证明:(1)取AC的中点E,连接ME,NE,则ME∥SA又∵SA⊥平面ABC,
∴ME⊥平面ABC
∴NE为MN在平面ABC内的射影
又∵N,E分别为AB,AC的中点
∴NE∥BC
∴NE⊥AB
由三垂线定理知MN⊥AB
(2)过A作AF⊥DN与DN的延长线相交于点F,连接SF
由三垂线定理知,∠SFA即为二面角S-ND-A的平面角
在Rt△DBN中,tan∠DNB=
| DB |
| BN |
| 1 |
| 2 |
∴sin∠DNB=
| ||
| 5 |
在Rt△AFN中,NF=AN•sin∠DNB=
2
| ||
| 5 |
在Rt△SAF中,tan∠SFA=
| SA |
| AF |
| 5 |
∴cos∠SFA=
| ||
| 6 |
即二面角S-ND-A的余弦值为
| ||
| 6 |
(3)过点A作AH⊥SF于H
由(2)知平面SAF⊥平面SND
∴AH⊥平面SND
∴AH的长即为点A到平面SND的距离
在Rt△AHF中,AH=AF•sin∠SAF=
2
| ||
| 5 |
| ||
| 6 |
| ||
| 3 |
故点A到平面SND的距离为
| ||
| 3 |
点评:本题考查的知识点是二面角的平面角及求法,直线与直线垂直的判定,点到平面的距离,(1),(2)的关键是熟练掌握三垂直定理,而(3)的关键是根据(2)的结合得到AH的长即为点A到平面SND的距离.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
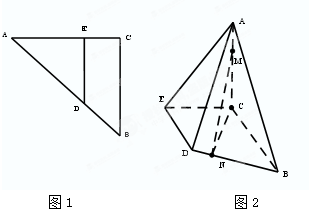 如图,△ABC是以∠C为直角的等腰直角三角形,直角边长为8,DE∥BC,AE:EC=5:3,沿DE将△ADE折起使得点A在平面BCED上的射影是点C,
如图,△ABC是以∠C为直角的等腰直角三角形,直角边长为8,DE∥BC,AE:EC=5:3,沿DE将△ADE折起使得点A在平面BCED上的射影是点C,