题目内容
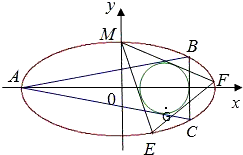 如图,已知圆G:(x-2)2+y2=r2是椭圆
如图,已知圆G:(x-2)2+y2=r2是椭圆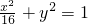 的内接△ABC的内切圆,其中A为椭圆的左顶点,
的内接△ABC的内切圆,其中A为椭圆的左顶点,
(1)求圆G的半径r;
(2)过点M(0,1)作圆G的两条切线交椭圆于E,F两点,证明:直线EF与圆G相切.
解:(1)设B(2+r,y0),过圆心G作GD⊥AB于D,BC交长轴于H
由 得
得 ,
,
即 (1)
(1)
而点B(2+r,y0)在椭圆上, (2)
(2)
由(1)、(2)式得15r2+8r-12=0,
解得 或
或 (舍去)
(舍去)
(2)设过点M(0,1)与圆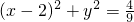 相切的直线方程为:y-1=kx(3)
相切的直线方程为:y-1=kx(3)
则 ,即32k2+36k+5=0(4)
,即32k2+36k+5=0(4)
解得
将(3)代入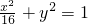 得(16k2+1)x2+32kx=0,
得(16k2+1)x2+32kx=0,
则异于零的解为
设F(x1,k1x1+1),E(x2,k2x2+1),
则
则直线FE的斜率为:
于是直线FE的方程为:
即
则圆心(2,0)到直线FE的距离
故结论成立.
分析:(1)可取BC⊥X轴时来研究,则可设B(2+r,y0),过圆心G作GD⊥AB于D,BC交长轴于H由 即
即 ,再由点B(2+r,y0)在椭圆上,建立关于r的方程求解.
,再由点B(2+r,y0)在椭圆上,建立关于r的方程求解.
(2)设过点M(0,1)与圆相切的直线方程为:y-1=kx,由圆心到直线的距离等于半径求 ,与椭圆方程联立,表示出E,F和坐标,从而得到EF所在的直线的方程,再探讨圆心到直线的距离和半径的关系.
,与椭圆方程联立,表示出E,F和坐标,从而得到EF所在的直线的方程,再探讨圆心到直线的距离和半径的关系.
点评:本题主要是通过圆和椭圆来考查直线和圆,直线和椭圆的位置关系.
由
 得
得 ,
,即
 (1)
(1)而点B(2+r,y0)在椭圆上,
 (2)
(2)由(1)、(2)式得15r2+8r-12=0,
解得
 或
或 (舍去)
(舍去)(2)设过点M(0,1)与圆
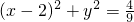 相切的直线方程为:y-1=kx(3)
相切的直线方程为:y-1=kx(3)则
 ,即32k2+36k+5=0(4)
,即32k2+36k+5=0(4)解得

将(3)代入
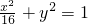 得(16k2+1)x2+32kx=0,
得(16k2+1)x2+32kx=0,则异于零的解为

设F(x1,k1x1+1),E(x2,k2x2+1),
则

则直线FE的斜率为:

于是直线FE的方程为:

即

则圆心(2,0)到直线FE的距离

故结论成立.
分析:(1)可取BC⊥X轴时来研究,则可设B(2+r,y0),过圆心G作GD⊥AB于D,BC交长轴于H由
 即
即 ,再由点B(2+r,y0)在椭圆上,建立关于r的方程求解.
,再由点B(2+r,y0)在椭圆上,建立关于r的方程求解.(2)设过点M(0,1)与圆相切的直线方程为:y-1=kx,由圆心到直线的距离等于半径求
 ,与椭圆方程联立,表示出E,F和坐标,从而得到EF所在的直线的方程,再探讨圆心到直线的距离和半径的关系.
,与椭圆方程联立,表示出E,F和坐标,从而得到EF所在的直线的方程,再探讨圆心到直线的距离和半径的关系.点评:本题主要是通过圆和椭圆来考查直线和圆,直线和椭圆的位置关系.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
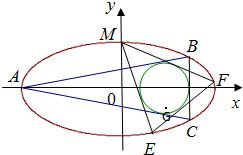 如图,已知圆G:(x-2)2+y2=r2是椭圆
如图,已知圆G:(x-2)2+y2=r2是椭圆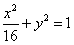 的内接△ABC的内切圆, 其中A为椭圆的左顶点。
的内接△ABC的内切圆, 其中A为椭圆的左顶点。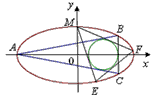
 的内接△ABC的内切圆,其中A为椭圆的左顶点,
的内接△ABC的内切圆,其中A为椭圆的左顶点,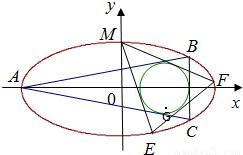
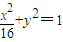 的内接△ABC的内切圆,其中A为椭圆的左顶点,
的内接△ABC的内切圆,其中A为椭圆的左顶点,