题目内容
10.在△ABC中,a=7,b=3,c=8,求A和S△ABC.分析 根据余弦定理求出其中的一个夹角,利用三角形的面积公式,即可得到结论.
解答 解:∵a=7,b=3,c=8,
∴由余弦定理得cosA=$\frac{{3}^{2}+{8}^{2}-{7}^{2}}{2×3×8}$=$\frac{1}{2}$,
∴sinA=$\frac{\sqrt{3}}{2}$,
∵a<c,∴$A=\frac{π}{3}$
S△ABC=$\frac{1}{2}bcsinA$=$\frac{1}{2}×3×8×\frac{\sqrt{3}}{2}$=6$\sqrt{3}$.
点评 本题主要考查三角形的面积的计算以及余弦定理的应用,要求熟练掌握相应的公式.

练习册系列答案
相关题目
18.设函数f(x)=$\left\{\begin{array}{l}{2-x,0≤x≤1}\\{(x-2)^{2},1<x≤2}\end{array}\right.$,则f[f($\frac{3}{2}$)]的值等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{9}{4}$ |
5.设f(x)=-m(m+e)x2,g(x)=x2+(m-1)x-m,命题p:?x0∈R,使得f(x0)<0或g(x0)<0,则实数m的取值范围是( )
| A. | {m|-e≤m≤0} | B. | {m|0≤m≤e} | C. | {m∈R|m≠-1} | D. | {-1} |
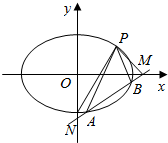 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{3}}}{2}$,过椭圆C上一点P(2,1)作倾斜角互补的两条直线,分别与椭圆交于点A、B,直线AB与x轴交于点M,与y轴负半轴交于点N.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{3}}}{2}$,过椭圆C上一点P(2,1)作倾斜角互补的两条直线,分别与椭圆交于点A、B,直线AB与x轴交于点M,与y轴负半轴交于点N.