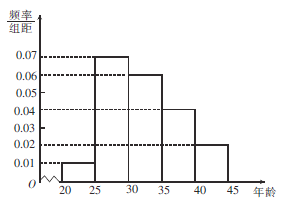
题目内容
【题目】已知数列![]() ,前n项和为
,前n项和为![]() ,对任意的正整数n,都有
,对任意的正整数n,都有![]() 恒成立.
恒成立.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知关于n的不等式![]() …
…![]() 对一切
对一切![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)已知 ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小并证明.
的大小并证明.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,证明见解析.
,证明见解析.
【解析】
(1)利用数列的递推关系式化简,通过累积法转化求解数列的通项公式.
(2)设![]() ,利用后一项与前一项的差的符号,判断数列的单调性即可.
,利用后一项与前一项的差的符号,判断数列的单调性即可.
(3)通过放缩法,利用裂项消项法求解数列的和Tn=c1+c2+c3+…+cn然后推出结果.
(1)由题意,因为2Sn=(n+1)an,
当n≥2时,2Sn-1=nan-1,
两式相减2an=(n+1)an-nan-1,可得(n-1)an=nan-1(n≥2),
又a1=1≠0,则an≠0,所以![]() ,
,
可得![]() ,
,
累乘得n≥2时,![]() ,
,
n=1时,a1=1也满足上式,
所以数列![]() 的通项公式为an=n
的通项公式为an=n![]() .
.
(2)设![]() ,
,
则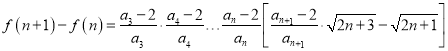
=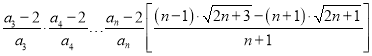
= ,
,
所以f(n)在n≥3,n∈N*上单调递减,
所以![]() ,即
,即![]() .
.
(3)![]() ,
,
则Tn=c1+c2+c3+…+cn
=![]()
=![]() .
.
所以![]() .
.

练习册系列答案
相关题目