题目内容
【题目】已知![]() 前
前![]() 项和
项和![]() 满足下列关系,求
满足下列关系,求![]() .
.
(1)![]() ;
;
(2)![]() ,且
,且![]() ,求
,求![]() ;
;
(3)![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)
;(2)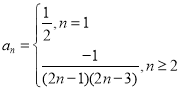 ;(3)
;(3)![]()
【解析】
(1)由题意![]() 类比写出
类比写出![]() ,两式相减可以整理得出
,两式相减可以整理得出![]() ,之后利用累乘法求得结果;
,之后利用累乘法求得结果;
(2)根据数列项与和的关系,将![]() 转化为
转化为![]() ,进一步整理得出
,进一步整理得出![]() ,利用等差数列通项公式求得
,利用等差数列通项公式求得![]() ,进而得到
,进而得到![]() ,之后利用
,之后利用![]() 的关系求得通项公式;
的关系求得通项公式;
(3)根据![]() 类比写出
类比写出![]() ,两式相减,整理得出
,两式相减,整理得出![]() ,验证
,验证![]() ,得出数列
,得出数列![]() 是以
是以![]() 为首项,以2为公比的等比数列,进而求得结果.
为首项,以2为公比的等比数列,进而求得结果.
(1)因为![]() ,
,
所以![]() ,
,
两式相减得![]() ,
,
整理得![]() ,即
,即![]() ,
,
所以有![]() ,
,
(2)由![]() 可得
可得![]() ,
,
整理得![]() ,即
,即![]() ,
,
又因为![]() ,
,
所以数列![]() 是以2为首项,以4为公差的等差数列,
是以2为首项,以4为公差的等差数列,
所以![]() ,所以
,所以![]() ,
,
所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,上式不成立,
,上式不成立,
所以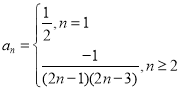
(3)由![]() 可得
可得![]() ,
,
两式相减得![]() ,整理得
,整理得![]() ,
,
即![]() ,且
,且![]() ,满足
,满足![]() ,
,
所以数列![]() 是以
是以![]() 为首项,以2为公比的等比数列,所以
为首项,以2为公比的等比数列,所以![]() ,
,
所以![]() .
.

【题目】(2015全国高考试题)某公司为了解用户对其产品的满意度,从![]() ,
,![]() 两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
![]() 地区:62 73 81 92 95 85 74 64 53 76
地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
![]() 地区:73 83 62 51 91 46 53 73 64 82
地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
根据用户满意度评分,将用户的满意度从低到高分为三个不同等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件![]() :“
:“![]() 地区用户的满意度等级高于
地区用户的满意度等级高于![]() 地区用户的满意度等级”假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求
地区用户的满意度等级”假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求![]() 的概率.
的概率.
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意,仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了![]() ,
,![]() 两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对
两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对![]() ,
,![]() 两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
|
| |
男业主 | 35 | 15 |
女业主 | 25 | 25 |
(1)分别估计![]() ,
,![]() 方案获得业主投票的概率;
方案获得业主投票的概率;
(2)判断能否有95%的把握认为投票选取管理方案与性别有关.
附: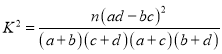 .
.
|
|
|
|
|
|
|
|