题目内容
已知数列{an}中,a1=2,an+1=2an+3.(Ⅰ)求a2,a3,a4;
(Ⅱ)证明{an+3}是等比数列
(Ⅲ)求数列{an}的通项公式.
【答案】分析:(Ⅰ)分别令n=2,n=3,n=4即可求得;
(Ⅱ)由an+1=2an+3,得an+1+3=2(an+3),根据等比数列的定义可作出证明;
(Ⅲ)由(Ⅱ)知,an+3=5•2n-1,变形可得an;
解答:(Ⅰ)解:由an+1=2an+3得,a2=2a1+3=7,a3=2a2+3=17,a4=2a3+3=37;
(Ⅱ)由an+1=2an+3,得an+1+3=2(an+3),
又a1+3=5,知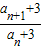 =2,
=2,
所以数列{an+3}是以5为首项,2为公比的等比数列.
(Ⅲ)解:由(Ⅱ)知,an+3=5•2n-1,
所以an=5•2n-1-3;
点评:本题考查数列递推式、数列求和、等比数列的定义等知识,考查学生综合运用知识解决问题的能力.
(Ⅱ)由an+1=2an+3,得an+1+3=2(an+3),根据等比数列的定义可作出证明;
(Ⅲ)由(Ⅱ)知,an+3=5•2n-1,变形可得an;
解答:(Ⅰ)解:由an+1=2an+3得,a2=2a1+3=7,a3=2a2+3=17,a4=2a3+3=37;
(Ⅱ)由an+1=2an+3,得an+1+3=2(an+3),
又a1+3=5,知
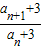 =2,
=2,所以数列{an+3}是以5为首项,2为公比的等比数列.
(Ⅲ)解:由(Ⅱ)知,an+3=5•2n-1,
所以an=5•2n-1-3;
点评:本题考查数列递推式、数列求和、等比数列的定义等知识,考查学生综合运用知识解决问题的能力.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|