题目内容
如题图已知椭圆C: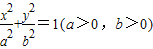 的上、下顶点分别为A、B,右焦点为F,△FAB是边长为2的等边三角形.
的上、下顶点分别为A、B,右焦点为F,△FAB是边长为2的等边三角形.(I)求椭圆C的方程;
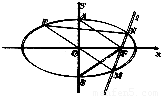
(II)设过点F的直线l交椭圆C于M、N两点,连接MO(O为坐标原点)并延长交椭圆C于点P,求△PMN的面积S△PMN的最大值.
【答案】分析:(Ⅰ)利用已知及椭圆的标准方程及性质即可得出;
(Ⅱ)把直线l的方程与椭圆的方程联立,利用根与系数的关系及三角形的面积公式、基本不等式的性质即可得出.
解答:解:(Ⅰ)由题意可得:b=1,a=2.
∴椭圆的方程为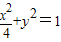 .
.
(Ⅱ)由椭圆的对称性可知:点M、P关于点O中心对称,∴S△PMN=2S△OMN.
由(Ⅰ)可知: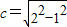 =
=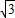 ,∴F
,∴F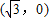 .
.
设直线l的方程为:x=my+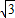 ,联立得
,联立得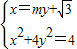 ,消去x得到
,消去x得到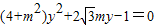 ,
,
∴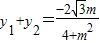 ,
,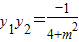 .
.
∴|y1-y2|=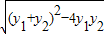 =
=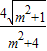 .
.
∴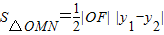 =
=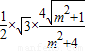 .
.
设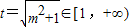 ,则
,则 =
=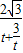
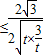 =1,当且仅当
=1,当且仅当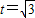 时取等号.
时取等号.
∴S△PMN≤2,即△PMN的面积的最大值为2.
点评:熟练掌握椭圆的标准方程及性质、直线与椭圆相交问题、根与系数的关系、三角形的面积公式、基本不等式的性质是解题的关键.
(Ⅱ)把直线l的方程与椭圆的方程联立,利用根与系数的关系及三角形的面积公式、基本不等式的性质即可得出.
解答:解:(Ⅰ)由题意可得:b=1,a=2.
∴椭圆的方程为
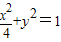 .
.(Ⅱ)由椭圆的对称性可知:点M、P关于点O中心对称,∴S△PMN=2S△OMN.
由(Ⅰ)可知:
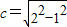 =
=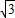 ,∴F
,∴F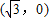 .
.设直线l的方程为:x=my+
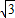 ,联立得
,联立得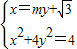 ,消去x得到
,消去x得到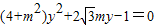 ,
,∴
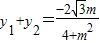 ,
,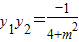 .
.∴|y1-y2|=
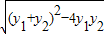 =
=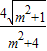 .
.∴
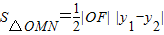 =
=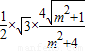 .
.设
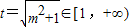 ,则
,则 =
=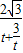
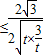 =1,当且仅当
=1,当且仅当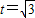 时取等号.
时取等号.∴S△PMN≤2,即△PMN的面积的最大值为2.
点评:熟练掌握椭圆的标准方程及性质、直线与椭圆相交问题、根与系数的关系、三角形的面积公式、基本不等式的性质是解题的关键.

练习册系列答案
相关题目
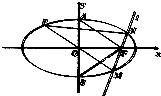 如题图已知椭圆C:
如题图已知椭圆C: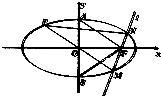 如题图已知椭圆C:
如题图已知椭圆C: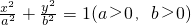 的上、下顶点分别为A、B,右焦点为F,△FAB是边长为2的等边三角形.
的上、下顶点分别为A、B,右焦点为F,△FAB是边长为2的等边三角形.