题目内容
设F1、F2分别是椭圆C:(1)当P∈C,且![]() =0,|PF1|·|PF2|=4时,求椭圆C的左、右焦点F1、F2;
=0,|PF1|·|PF2|=4时,求椭圆C的左、右焦点F1、F2;
(2)F1、F2是(1)中的椭圆的左、右焦点,已知⊙F2的半径是1,过动点Q的作⊙F2的切线QM,使得|QF1|=|QM|(M是切点),如图所示,求动点Q的轨迹方程.
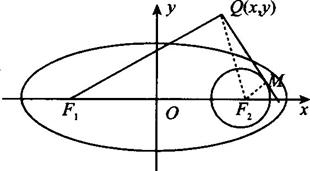
第19题图
答案:(1)∵c2=a2-b2,∴c2=4m2.又∵![]() =0
=0
∴PF1⊥PF2,
∴|PF1|2+|PF2|2=(2c)2=16m2
由椭圆定义可知|PF1|+|PF2|=2a=![]() ,
,
(|PF1|+|PF2|)2=16m2+8=24m2
从而得m2=1,c2=4m2=4,c=2.
∴F1(-2,0)、F2(2,0).
(2)∵F1(-2,0),F2(2,0),
由已知得|QF1|=![]() |QM|,即|QF1|2=2|QM|2,所以
|QM|,即|QF1|2=2|QM|2,所以
有|QF1|2=2(|QF2|2-1),
设Q(x,y),则(x+2)2+y2=2[(x-2)2+y2-1]
即(x-6)2+y2=32(或x2+y2-12x+4=0)
综上所述,所求轨迹方程为(x-6)2+y2=32.

练习册系列答案
相关题目
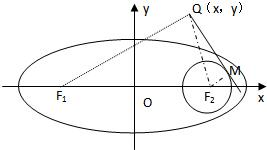 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C: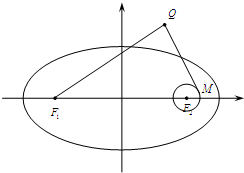 设F1、F2分别是椭圆
设F1、F2分别是椭圆