题目内容
已知平面区域D={(x,y)|-1≤x≤2,-1≤y≤2},z=ax+y(a是常数),?P(x0,y0)∈D,记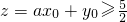 为事件A,则使
为事件A,则使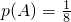 的常数a有
的常数a有
- A.0个
- B.1个
- C.2个
- D.3个以上
C
分析:.本题拟采用判断的方法求解,作出如图的图象,可以得出,这样的直线有两种类型,如图的虚、实两直线,事件A中的不等式过定点(0, ),故直接研究此点与矩形下部两个顶点的连线,看所得的三角形面积是否大于事件A所对应的面积即可
),故直接研究此点与矩形下部两个顶点的连线,看所得的三角形面积是否大于事件A所对应的面积即可
解答: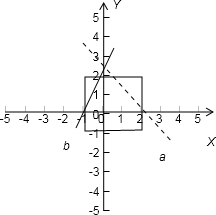 解:由题设条件知,
解:由题设条件知,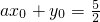 过定点(0,
过定点(0, )故直线
)故直线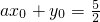 的情形有二,如图中的实线与虚线
的情形有二,如图中的实线与虚线
∵记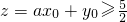 为事件A,则使
为事件A,则使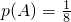 ,故点符合条件的点P(x0,y0)所在的区域面积为
,故点符合条件的点P(x0,y0)所在的区域面积为
右图中的虚线一定在某个位置使得事件A成立,故常数a必有一个
下验证实线情况是否能保证事件A成立,验证标准是当实线所对应的直线,即其斜率大于0时,符合条件的区域的面积是否有可能等于 ,若能,则常数a必有二个,否则就只有一个.
,若能,则常数a必有二个,否则就只有一个.
由于斜率大于0时,a<0,可判断得,事件A对应的区域应是实直线的上部,令直线过点(-1,1),验证此时实直线上部的面积是否大于或等于 ,此时直线的方程为
,此时直线的方程为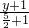 =
=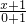 ,即y+1=
,即y+1= (x+1),令y=2,得x=-
(x+1),令y=2,得x=- ,故此时实直线上方的三角形的面积是
,故此时实直线上方的三角形的面积是
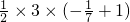 =
=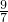 >
> 故存在这样的实直线使得事件A的概率等于
故存在这样的实直线使得事件A的概率等于
综上,存在两条这样的直线,故常数a的值有二
故选C
点评:.本题考查几何概率模型,求解本题的关键是把事件所对应的测试研究清楚,如本题要从事件对应的面积着手,本题中的条件下,利用事件A对应的面积求参数的值,计算量太大,故本题采取了判断的方法,改定量计算为定性判断,灵活选择方法可以大大降低题目难度.
分析:.本题拟采用判断的方法求解,作出如图的图象,可以得出,这样的直线有两种类型,如图的虚、实两直线,事件A中的不等式过定点(0,
 ),故直接研究此点与矩形下部两个顶点的连线,看所得的三角形面积是否大于事件A所对应的面积即可
),故直接研究此点与矩形下部两个顶点的连线,看所得的三角形面积是否大于事件A所对应的面积即可解答:
 解:由题设条件知,
解:由题设条件知,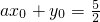 过定点(0,
过定点(0, )故直线
)故直线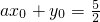 的情形有二,如图中的实线与虚线
的情形有二,如图中的实线与虚线∵记
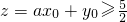 为事件A,则使
为事件A,则使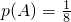 ,故点符合条件的点P(x0,y0)所在的区域面积为
,故点符合条件的点P(x0,y0)所在的区域面积为
右图中的虚线一定在某个位置使得事件A成立,故常数a必有一个
下验证实线情况是否能保证事件A成立,验证标准是当实线所对应的直线,即其斜率大于0时,符合条件的区域的面积是否有可能等于
 ,若能,则常数a必有二个,否则就只有一个.
,若能,则常数a必有二个,否则就只有一个.由于斜率大于0时,a<0,可判断得,事件A对应的区域应是实直线的上部,令直线过点(-1,1),验证此时实直线上部的面积是否大于或等于
 ,此时直线的方程为
,此时直线的方程为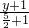 =
=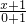 ,即y+1=
,即y+1= (x+1),令y=2,得x=-
(x+1),令y=2,得x=- ,故此时实直线上方的三角形的面积是
,故此时实直线上方的三角形的面积是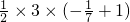 =
=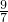 >
> 故存在这样的实直线使得事件A的概率等于
故存在这样的实直线使得事件A的概率等于
综上,存在两条这样的直线,故常数a的值有二
故选C
点评:.本题考查几何概率模型,求解本题的关键是把事件所对应的测试研究清楚,如本题要从事件对应的面积着手,本题中的条件下,利用事件A对应的面积求参数的值,计算量太大,故本题采取了判断的方法,改定量计算为定性判断,灵活选择方法可以大大降低题目难度.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目