题目内容
已知椭圆 (a>b>0)满足
(a>b>0)满足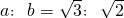 ,且椭圆C1过点
,且椭圆C1过点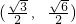 .
.
(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆C1的长轴,动直线l2垂直于l1且与l1交于点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;
(3)设曲线C2与x轴交于点Q,C2上有与Q不重合的不同两点R(x1,y1)、S(x2,y2),且满足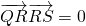 ,求点S的横坐标x2的取值范围.
,求点S的横坐标x2的取值范围.
解:(1)由已知,可设 ,
, (k>0),
(k>0),
所以椭圆C1的方程为 ,…(2分)
,…(2分)
因为椭圆C1过点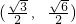 ,所以有
,所以有 ,解得k=1,…(3分)
,解得k=1,…(3分)
所以椭圆C1的方程为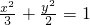 .…(4分)
.…(4分)
(2)F1(-1,0),F2(1,0),所以直线l1的方程为x=-1,…(5分)
由题意,|MP|=|MF2|,所以点M的轨迹C2是以F2为焦点,直线l1为准线的抛物线,
所以轨迹C2的方程是y2=4x. …(10分)
(3)Q(0,0),设 ,
, ,
,
所以 ,
, ,
,
因为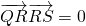 ,所以
,所以 ,…(12分)
,…(12分)
因为y1≠y2,y1≠0,化简得 ,…(15分)
,…(15分)
所以 ,当且仅当
,当且仅当 ,y1=±4时等号成立.…(16分)
,y1=±4时等号成立.…(16分)
所以 ,点S的横坐标的取值范围是[16,+∞).…(18分)
,点S的横坐标的取值范围是[16,+∞).…(18分)
分析:(1)设 ,
, (k>0),所以椭圆C1的方程为
(k>0),所以椭圆C1的方程为 ,由椭圆C1过点
,由椭圆C1过点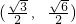 ,解得k=1,由此能求出椭圆C1的方程.
,解得k=1,由此能求出椭圆C1的方程.
(2)F1(-1,0),F2(1,0),所以直线l1的方程为x=-1,由|MP|=|MF2|,知点M的轨迹C2是以F2为焦点,直线l1为准线的抛物线,由此能求出轨迹C2的方程.
(3)Q(0,0),设 ,
, ,所以
,所以 ,
, ,因为
,因为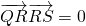 ,所以
,所以 ,化简得
,化简得 ,由此能求出点S的横坐标的取值范围是[16,+∞).
,由此能求出点S的横坐标的取值范围是[16,+∞).
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 ,
, (k>0),
(k>0),所以椭圆C1的方程为
 ,…(2分)
,…(2分)因为椭圆C1过点
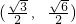 ,所以有
,所以有 ,解得k=1,…(3分)
,解得k=1,…(3分)所以椭圆C1的方程为
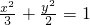 .…(4分)
.…(4分)(2)F1(-1,0),F2(1,0),所以直线l1的方程为x=-1,…(5分)
由题意,|MP|=|MF2|,所以点M的轨迹C2是以F2为焦点,直线l1为准线的抛物线,
所以轨迹C2的方程是y2=4x. …(10分)
(3)Q(0,0),设
 ,
, ,
,所以
 ,
, ,
,因为
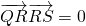 ,所以
,所以 ,…(12分)
,…(12分)因为y1≠y2,y1≠0,化简得
 ,…(15分)
,…(15分)所以
 ,当且仅当
,当且仅当 ,y1=±4时等号成立.…(16分)
,y1=±4时等号成立.…(16分)所以
 ,点S的横坐标的取值范围是[16,+∞).…(18分)
,点S的横坐标的取值范围是[16,+∞).…(18分)分析:(1)设
 ,
, (k>0),所以椭圆C1的方程为
(k>0),所以椭圆C1的方程为 ,由椭圆C1过点
,由椭圆C1过点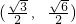 ,解得k=1,由此能求出椭圆C1的方程.
,解得k=1,由此能求出椭圆C1的方程.(2)F1(-1,0),F2(1,0),所以直线l1的方程为x=-1,由|MP|=|MF2|,知点M的轨迹C2是以F2为焦点,直线l1为准线的抛物线,由此能求出轨迹C2的方程.
(3)Q(0,0),设
 ,
, ,所以
,所以 ,
, ,因为
,因为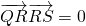 ,所以
,所以 ,化简得
,化简得 ,由此能求出点S的横坐标的取值范围是[16,+∞).
,由此能求出点S的横坐标的取值范围是[16,+∞).点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.