题目内容
已知关于x的方程4x2-2(m+1)x+m=0的两个根恰好是一个直角三角形的两个锐角的余弦,求实数m的值.

设直角三角形的两个锐角分别为α、β,则可得α+β= ,
,
∴cosα=sinβ
∵方程4x2-2(m+1)x+m=0中,Δ=4(m+1)2-4·4m=4(m-1)2≥0
∴当m∈R,方程恒有两实根.
又∵cosα+cosβ=sinβ+cosβ= ,cosα·cosβ=sinβcosβ=
,cosα·cosβ=sinβcosβ=
∴由以上两式及sin2β+cos2β=1,得1+2· =(
=( )2
)2
解得m=±
当m= 时,cosα+cosβ=
时,cosα+cosβ= >0,cosα·cosβ=
>0,cosα·cosβ= >0,满足题意,
>0,满足题意,
当m=- 时,cosα+cosβ=
时,cosα+cosβ= <0,这与α、β是锐角矛盾,应舍去.
<0,这与α、β是锐角矛盾,应舍去.
综上,m=
 ,
,∴cosα=sinβ
∵方程4x2-2(m+1)x+m=0中,Δ=4(m+1)2-4·4m=4(m-1)2≥0
∴当m∈R,方程恒有两实根.
又∵cosα+cosβ=sinβ+cosβ=
 ,cosα·cosβ=sinβcosβ=
,cosα·cosβ=sinβcosβ=
∴由以上两式及sin2β+cos2β=1,得1+2·
 =(
=( )2
)2解得m=±

当m=
 时,cosα+cosβ=
时,cosα+cosβ= >0,cosα·cosβ=
>0,cosα·cosβ= >0,满足题意,
>0,满足题意,当m=-
 时,cosα+cosβ=
时,cosα+cosβ= <0,这与α、β是锐角矛盾,应舍去.
<0,这与α、β是锐角矛盾,应舍去.综上,m=


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象过点(0,-3),且
的图象过点(0,-3),且 的解集
的解集 .
. 的解析式;
的解析式; 的最值.
的最值. =2,求下列各式的值:
=2,求下列各式的值: ;
; ;
;
 等于
等于



 =()
=() 


 ,
, ,那么
,那么 的值是( ).
的值是( ).



 是关于
是关于 的方程
的方程 的两个实根,且
的两个实根,且 ,求
,求 的值
的值
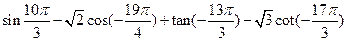 的值__________.
的值__________.