题目内容
解下列不等式:(1)
思路分析:由于“a>b>0![]() a2>b2”,所以在不等式两边平方时,必须要注意两边是否均大于或等于零,还要注意根号下大于或等于零.因此对(1)有2-x≥0;而在(2)中当3-2x<0时,只要3-x≥0即可.
a2>b2”,所以在不等式两边平方时,必须要注意两边是否均大于或等于零,还要注意根号下大于或等于零.因此对(1)有2-x≥0;而在(2)中当3-2x<0时,只要3-x≥0即可.
解:(1)原不等式化为
即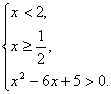 即
即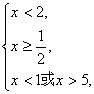
∴![]() ≤x<1.故原不等式的解为
≤x<1.故原不等式的解为![]() ≤x<1.
≤x<1.
(2)原不等式化为![]() 或
或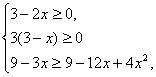 即
即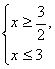 或
或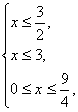
即![]() ≤x≤3或0≤x≤
≤x≤3或0≤x≤![]() .
.
故原不等式的解为0≤x≤3.
思维启示:解![]() ≥g(x)类型的不等式需要根据性质a>b>0
≥g(x)类型的不等式需要根据性质a>b>0![]() a2>b2.故两边平方时需要对g(x)是否大于零进行分类讨论,即转化为
a2>b2.故两边平方时需要对g(x)是否大于零进行分类讨论,即转化为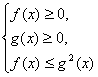 或
或![]() 去解.
去解.

练习册系列答案
相关题目
 ; 2
; 2 ;
; ; 4
; 4 .
. >0;
(2)9x2-6x+1≥0.
>0;
(2)9x2-6x+1≥0.