题目内容
已知函数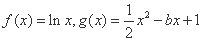 (
(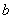 为常数).
为常数).
(1)函数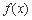 的图象在点(
的图象在点(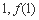 )处的切线与函数
)处的切线与函数 的图象相切,求实数
的图象相切,求实数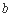 的值;
的值;
(2)若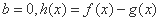 ,
,
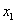 、
、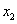
 使得
使得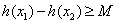 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数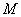 ;
;
(3)当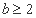 时,若对于区间[1,2]内的任意两个不相等的实数
时,若对于区间[1,2]内的任意两个不相等的实数 ,
, ,都有
,都有
 成立,求
成立,求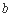 的取值范围.
的取值范围.
解:(1)∵ ,∴
,∴ ,
, ,
,
∴函数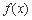 的图象在点(
的图象在点(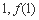 )处的切线方程为
)处的切线方程为 ,-
,-
∵直线 与函数
与函数 的图象相切,由
的图象相切,由 消去y得
消去y得 ,
,
则 ,解得
,解得 -
-
(2)当 时,∵
时,∵ ,
,
∴ ,
,
当 时,
时, ,∴在
,∴在 上单调递减,
上单调递减,
 ,
,
则
 ,
,
∴
 ,故满足条件的最大整数
,故满足条件的最大整数 .-
.-
(3)不妨设 ,∵函数
,∵函数 在区间[1,2]上是增函数,∴
在区间[1,2]上是增函数,∴ ,
,
∵函数 图象的对称轴为
图象的对称轴为 ,且
,且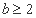 ,∴函数
,∴函数 在区间[1,2]上是减函数,
在区间[1,2]上是减函数,
∴
∴ 等价于
等价于 ,
,
即 ,
,
等价于 在区间[1,2]上是增函数,
在区间[1,2]上是增函数,
等价于 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,
等价于 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,
∴ ,又
,又 ,∴
,∴

练习册系列答案
相关题目
 (S2n+S2m)-(
(S2n+S2m)-( n-m)2,其中m,n为任意正整数.
n-m)2,其中m,n为任意正整数. -
-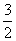 an+33=k2的所有正整数k,n.
an+33=k2的所有正整数k,n.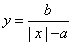
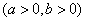 的函数称为“莫言函数”,并把其与y轴的交点关于原
的函数称为“莫言函数”,并把其与y轴的交点关于原 的解集为 .
的解集为 . 中,已知
中,已知 且
且 .
. 的值;
的值; ,求边AC的长.
,求边AC的长. ”是“函数
”是“函数 为奇函数”的
为奇函数”的  人分配
人分配 种.(用数字作答)
种.(用数字作答) 与直线
与直线 平行,则
平行,则 ______ .
______ . _________.
_________.