题目内容
 如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
(1)求|PA|+|PF|的最小值;
(2)求k的取值范围;
(3)若O为坐标原点,问是否存在点M,使过点M的动直线与抛物线交于B,C两点,且以BC为直径的圆恰过坐标原点,若存在,求出动点M的坐标;若不存在,请说明理由.
 解:如图,设抛物线的准线为l,过P作PB⊥l于B,过A作AC⊥l于C,
解:如图,设抛物线的准线为l,过P作PB⊥l于B,过A作AC⊥l于C,(1)由抛物线定义知|PF|=|PB|?|PA|+|PF|=|PA|+|PB|≥|AC|
(折线段大于垂线段),当且仅当A,P,C三点共线取等号.
由题意知|AC|=8,即?|PA|+|PF|的最小值是8(4分)
(2)
 (5分)
(5分)(3)假设存在点M,设过点M的直线方程为y=kx+b,
显然k≠0,b≠0,设B(x1,y1),C(x2,y2),由以BC为直径的圆恰过坐标
原点有
 ?x1x2+y1y2=0①(9分)
?x1x2+y1y2=0①(9分)把y=kx+b代入y2=16x得k2x2+2(bk-8)x+b2=0
由韦达定理
 .②
.②又y1y2=(kx1+b)(kx2+b)=k2x1x2+bk(x1+x2)+b2.③
②代入③得
 .④
.④②④代入①得
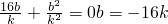 (12分)
(12分)?动直线方程为y=kx-16k=k(x-16)必过定点(16,0)
当kBC不存在时,直线x=16交抛物线于B(16,-16),C(16,16),仍然有
 ,
,综上:存在点M(16,0)满足条件(15分)
分析:(1)由抛物线定义知|PF|=|PB|?|PA|+|PF|=|PA|+|PB|≥|AC|,当且仅当A,P,C三点共线取等号.由题意知|PA|+|PF|的最小值是8.
(2)
 .
.(3)假设存在点M,设过点M的直线方程为y=kx+b,设B(x1,y1),C(x2,y2),由以BC为直径的圆恰过坐标原点有
 ,x1x2+y1y2=0,把y=kx+b代入y2=16x得k2x2+2(bk-8)x+b2=0,由韦达定理
,x1x2+y1y2=0,把y=kx+b代入y2=16x得k2x2+2(bk-8)x+b2=0,由韦达定理 .又y1y2=(kx1+b)(kx2+b)=k2x1x2+bk(x1+x2)+b2.由此知动直线方程为y=kx-16k=k(x-16)必过定点(16,0).
.又y1y2=(kx1+b)(kx2+b)=k2x1x2+bk(x1+x2)+b2.由此知动直线方程为y=kx-16k=k(x-16)必过定点(16,0).点评:本题考查直线的圆锥曲线的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和AB,OA分别交于C,D,且平分△AOB的面积,求CD的最小值.
如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和AB,OA分别交于C,D,且平分△AOB的面积,求CD的最小值.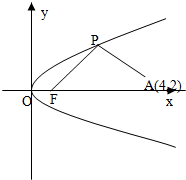 如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点. 如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和线段AB,OA分别交于C,D且平分△AOB的面积.
如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和线段AB,OA分别交于C,D且平分△AOB的面积.
