题目内容
 如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和线段AB,OA分别交于C,D且平分△AOB的面积.
如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和线段AB,OA分别交于C,D且平分△AOB的面积.(1)求△AOB的面积;
(2)求CD的最小值.
分析:(1)令直线l:3x+4y-12=0中y=0,求出x的值,即为A的横坐标,确定出A的坐标,令直线l解析式中x=0,求出y的值,即为B的纵坐标,确定出B的坐标,进而求出OA及OB的长,由三角形AOB为直角三角形,利用两直角边OA与OB乘积的一半即可求出三角形AOB的面积;
(2)设AD=m,AC=n,在直角三角形AOB中,由AO及OB的长,利用勾股定理求出AB的长,再利用锐角三角形函数定义求出sinA及cosA的值,由AD,AC及sinA的值,利用三角形的面积公式表示出三角形ACD的面积,根据直线CD平分三角形AOB的面积,由第一问求出的三角形AOB的面积求出三角形AOD的面积,整理后求出mn的值,在利用余弦定理表示出CD2=m2+n2-2mncosA,将mn及cosA的值代入,并利用基本不等式变形,再将mn的值代入,即可求出CD的最小值,以及此时m与n的值.
(2)设AD=m,AC=n,在直角三角形AOB中,由AO及OB的长,利用勾股定理求出AB的长,再利用锐角三角形函数定义求出sinA及cosA的值,由AD,AC及sinA的值,利用三角形的面积公式表示出三角形ACD的面积,根据直线CD平分三角形AOB的面积,由第一问求出的三角形AOB的面积求出三角形AOD的面积,整理后求出mn的值,在利用余弦定理表示出CD2=m2+n2-2mncosA,将mn及cosA的值代入,并利用基本不等式变形,再将mn的值代入,即可求出CD的最小值,以及此时m与n的值.
解答:解:(1)令y=0,求出x=4,∴A(4,0),
令x=0,求出y=3,∴B(0,3),
∴OA=4,OB=3,
则S△AOB=
OA•OB=
×4×3=6;
(2)设AD=m,AC=n,
在Rt△AOB中,OA=4,0B=3,
根据勾股定理得:AB=
=5,
∴sinA=
=
,又直线CD平分△AOB的面积,
∴S△ACD=
mnsinA=
×6=3,∴mn=10,
在△AOB中,cosA=
=
,
由余弦定理得:CD2=m2+n2-2mncosA=m2+n2-2×10×
=m2+n2-16≥2mn-16=4,
∴CD≥2,当且仅当m=n=
时取等号,
则CD的最小值为2.
令x=0,求出y=3,∴B(0,3),
∴OA=4,OB=3,
则S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
(2)设AD=m,AC=n,
在Rt△AOB中,OA=4,0B=3,
根据勾股定理得:AB=
| OA2+OB2 |
∴sinA=
| OB |
| AB |
| 3 |
| 5 |
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
在△AOB中,cosA=
| OA |
| AB |
| 4 |
| 5 |
由余弦定理得:CD2=m2+n2-2mncosA=m2+n2-2×10×
| 4 |
| 5 |
∴CD≥2,当且仅当m=n=
| 10 |
则CD的最小值为2.
点评:此题考查了三角形的面积公式,余弦定理,以及基本不等式的运用,熟练掌握公式及定理是解本题的关键.

练习册系列答案
相关题目
 如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和AB,OA分别交于C,D,且平分△AOB的面积,求CD的最小值.
如图所示,已知直线l:3x+4y-12=0与x,y轴的正半轴分别交于A,B两点,直线l1和AB,OA分别交于C,D,且平分△AOB的面积,求CD的最小值.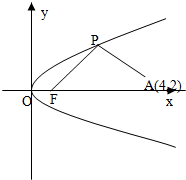 如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
