题目内容

在区间[10，20]内的所有实数中，随机取一个实数a，则a＜15的概率是________．

$\text{[math]}$
分析：在区间[10，20]内的所有实数不可数，属于几何概型，我们分别计算出区间[10，20]的长度，区间[10，15）的长度，代入几何概型概率计算公式，即可得到答案．
解答：由于试验的全部结果构成的区域长度为20-10=10，
构成该事件的区域长度为15-10=5，
所以概率为 $\text{[math]}$ = $\text{[math]}$
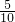故答案为： $\text{[math]}$
点评：本题主要考查几何概型的概率计算，其中根据已知条件计算出基本事件总数对应的几何量的大小，和满足条件的几何量的大小是解答本题的关键，属于基础题．

练习册系列答案

相关题目

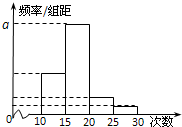对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表如下，频率分布直方图如图：

分组	频数	频率
[10，15）	10	0.25
[15，20）	25	a
[20，25）	m	p
[25，30）	2	0.05
合计	M	1

（Ⅰ）求出表中M，p及图中a的值；
（Ⅱ）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间[10，15）内的人数；
（Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间[20，25）内的概率．

编号为A₁，A₂，…，A₁₆的16名篮球运动员在某次训练比赛中的得分记录如下：

运动员编号	A₁	A₂	A₃	A₄	A₅	A₆	A₇	A₈
得分	15	35	21	28	25	36	18	34
运动员编号	A₉	A₁₀	A₁₁	A₁₂	A₁₃	A₁₄	A₁₅	A₁₆
得分	17	26	25	33	22	12	31	38

（Ⅰ）将得分在对应区间内的人数填入相应的空格；

区间	[10，20）	[20，30）	[30，40]
人数

（Ⅱ）从得分在区间[20，30）内的运动员中随机抽取2人，
（i）用运动员的编号列出所有可能的抽取结果；
（ii）求这2人得分之和大于50分的概率．

（2012•衡阳模拟）编号为A₁，A₂，…A₁₆的16名蓝球运动员在某次训练比赛中的得分记录如下：

运动员编号	A₁	A₂	A₃	A₄	A₅	A₆	A₇	A₈
得分	15	35	21	28	25	36	18	34
运动员编号	A₉	A₁₀	A₁₁	A₁₂	A₁₃	A₁₄	A₁₅	A₁₆
得分	17	26	25	33	22	12	31	38

（1）将得分在对应区间内的人数填入相应的空格；

区间	[10，20）	[20，30）	[30，40]
人数

（2）从得分在区间[20，30）内的运动员中随机抽取2人，用运动员的编号列出所有可能的抽取结果，并求这2人得分之和大于50分的概率．

在区间[10，20]内的所有实数中，随机取一个实数a，则这个实数a＜13的概率为

在区间[10，20]内的所有实数中，随机取一个实数a，则a＜15的概率是________．

试题分类