题目内容
在底面是直角梯形的四棱锥S—ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=2AD.求面SCD与面SBA所成的二面角的余弦值.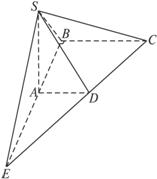
剖析:显然,本题中的二面角只有一个公共顶点,属“无棱二面角”,若从定义法入手,必须再找一个公共点,容易发现BA、CD相交,可得交点E,则SE为二面角的棱.
解法一:(定义法)如图,延长BA、CD交于E,连结SE,则SE为所求二面角的棱.

∵AD∥BC,BC=2AD,
∴EA=AB=SA.
∴△ESB是直角三角形,且SE⊥SB.
又BC⊥AB,BC⊥SA,∴BC⊥平面SBE.
∴SB是SC在面SBE上的射影.
∴SE⊥SC.
∠BSC是所求二面角的平面角.
在Rt△SAB中,易得SB=![]() AB.
AB.
在Rt△SBC中,SC=![]() =
=![]() AB.
AB.
cos∠BSC=![]() =
=![]() ,即面SCD与面SBA所成的二面角的余弦值为
,即面SCD与面SBA所成的二面角的余弦值为![]() .
.
解法二:(射影法)如上图,∵SA⊥面ABCD,∴SA⊥BC.
又AB⊥BC,∴BC⊥面SAB,而AD∥BC,
∴AD⊥面SAB.
∴△SDC在面SAB上的射影是△SAB.
于是cosθ=![]() .
.
∵SA=AB=BC=2AD,
∴SB=![]() AB,SC=
AB,SC=![]() AB.
AB.
SD=DC=![]() AB,
AB,
易求得△SDC中SC边上的高为![]() ,
,
∴S△SDC=![]() AB2,S△SAB=
AB2,S△SAB=![]() AB2.∴cosθ=
AB2.∴cosθ=![]() .
.
故所求二面角的余弦值是![]() .
.

练习册系列答案
相关题目
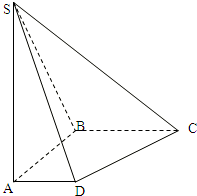 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=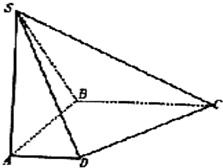 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,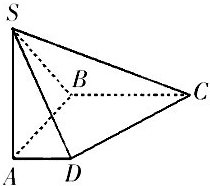 如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD, 如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.
如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1. (2010•宝山区模拟)在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
(2010•宝山区模拟)在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=