题目内容
设函数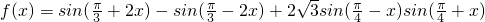
，
（Ⅰ）当f（x）取最小值时，求x的集合；
（Ⅱ）写出f（x）的单调递增区间．
解：（Ⅰ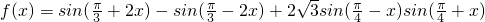）=sin2x+
cos2x
=2sin（2x+
），故当 2x+=2kπ-
，k∈z，即x=kπ-
时，k∈z，f（x）取最小值，
故x的集合为{x|x=kπ-，k∈z}．
（Ⅱ）由 kπ-≤2x+≤kπ+，k∈z，可得 kπ-≤x≤kπ+
z，
故f（x）的单调递增区间为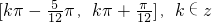
．
分析：（Ⅰ）利用两角和差的正弦公式化简函数f（x）的解析式为2sin（2x+），根据 2x+=2kπ-，解出x的值即为所求．
（Ⅱ）由 kπ-≤2x+≤kπ+，k∈z，解不等式可得x的范围即为f（x）的单调递增区间．
点评：本题考查两角和差的正弦公式的应用，正弦函数的单调性和最值，化简函数f（x）的解析式为2sin（2x+），是解题
的关键．
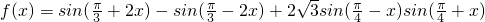=sin2x+cos2x=2sin（2x+
），故当 2x+=2kπ-，k∈z，即x=kπ-时，k∈z，f（x）取最小值，故x的集合为{x|x=kπ-
，k∈z}．（Ⅱ）由 kπ-
≤2x+≤kπ+，k∈z，可得 kπ-≤x≤kπ+ z，故f（x）的单调递增区间为
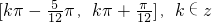．分析：（Ⅰ）利用两角和差的正弦公式化简函数f（x）的解析式为2sin（2x+
），根据 2x+=2kπ-，解出x的值即为所求．（Ⅱ）由 kπ-
≤2x+≤kπ+，k∈z，解不等式可得x的范围即为f（x）的单调递增区间．点评：本题考查两角和差的正弦公式的应用，正弦函数的单调性和最值，化简函数f（x）的解析式为2sin（2x+
），是解题的关键．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目