题目内容
16.已知函数f(x)=2x2ex与g(x)=3xex+a的图象有且只有两个公共点,则实数a的取值范围是a=$\frac{9\sqrt{e}}{{e}^{2}}$或-e<a≤0.分析 令a=h(x)=2x2ex-3xex,求导h′(x)=ex(2x+3)(x-1),从而确定函数的单调性及极值,从而结合图象解得.
解答 解:由题意得,2x2ex=3xex+a,
∴a=h(x)=2x2ex-3xex,
h′(x)=4xex+2x2ex-3ex-3xex
=ex(2x2+x-3)
=ex(2x+3)(x-1),
∴h(x)在(-∞,-$\frac{3}{2}$)上是增函数,在(-$\frac{3}{2}$,1)上是减函数,在(1,+∞)上是增函数;
且h(1)=-e,h(-$\frac{3}{2}$)=$\frac{9\sqrt{e}}{{e}^{2}}$,且$\underset{lim}{x→-∞}$h(x)=0,
故作h(x)=2x2ex-3xex的图象如下,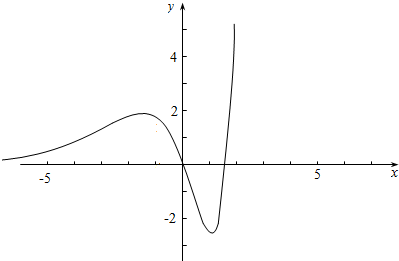
结合图象可知,实数a的取值范围是a=$\frac{9\sqrt{e}}{{e}^{2}}$或-e<a≤0.
故答案为:a=$\frac{9\sqrt{e}}{{e}^{2}}$或-e<a≤0.
点评 本题考查了导数的综合应用及数形结合的思想应用.

练习册系列答案
相关题目
6.已知两定点A(-2,0),B(1,0),若动点P满足|PA|=2|PB|,则P的轨迹为( )
| A. | 直线 | B. | 线段 | C. | 圆 | D. | 半圆 |
8.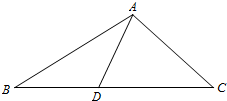 如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
 如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{3}}{6}$ |
6.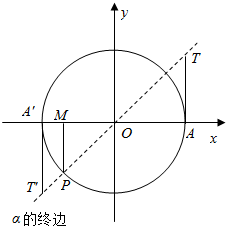 如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )
如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )
 如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )
如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )| A. | 正弦值是PM,正切线是A′T′ | B. | 正弦值是MP,正切线是A′T′ | ||
| C. | 正弦值是MP,正切线是AT | D. | 正弦值是PM,正切线是AT |