题目内容
若一个正四面体的表面积为S1,其内切球的表面积为S2,则 =________.
=________.

分析:设正四面体ABCD的棱长为a,利用体积分割法计算出内切球半径r=
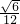 a,从而得到S2关于a的式子.利用正三角形面积公式,算出正四面体的表面积S1关于a的式子,由此不难得出S1与S2的比值.
a,从而得到S2关于a的式子.利用正三角形面积公式,算出正四面体的表面积S1关于a的式子,由此不难得出S1与S2的比值.解答:设正四面体ABCD的棱长为a,可得
∵等边三角形ABC的高等于
 a,底面中心将高分为2:1的两段
a,底面中心将高分为2:1的两段∴底面中心到顶点的距离为
 ×
× a=
a= a
a可得正四面体ABCD的高为h=
 =
= a
a∴正四面体ABCD的体积V=
 ×S△ABC×
×S△ABC× a=
a=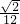 a2,
a2,设正四面体ABCD的内切球半径为r,则4×
 ×S△ABC×r=
×S△ABC×r=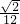 a2,解得r=
a2,解得r=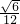 a
a∴内切球表面积S2=4πr2=

∵正四面体ABCD的表面积为S1=4×S△ABC=
 a2,
a2,∴
 =
= =
=
故答案为:

点评:本题给出正四面体,求它的表面积与其内切球表面积的比值,着重考查了正四面体的性质、球的表面积公式和多面体的外接、内切球算法等知识,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
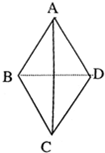 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A. 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A. .求
.求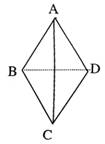 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A. .求
.求