题目内容
设函数f(x)= +log2
+log2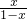 ,定义Sn=f(
,定义Sn=f( )+f(
)+f( )+…+f(
)+…+f( ),其中,n∈N+,n≥2,则Sn=
),其中,n∈N+,n≥2,则Sn=
- A.

- B.
 -log2(n-1)
-log2(n-1) - C.

- D.
 +log2(n-1)
+log2(n-1)
C
分析:根据所给函数,确定f(x)+f(1-x)=1,进而利用倒序相加,即可求得结论.
解答:∵f(x)= +log2
+log2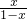 ,
,
∴f(1-x)= +log2
+log2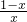 ,
,
∴f(x)+f(1-x)= +log2
+log2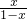 +
+ +log2
+log2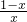 =1
=1
∵Sn=f( )+f(
)+f( )+…+f(
)+…+f( ),
),
∴Sn=f( )+f(
)+f(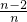 )+…+f(
)+…+f( )
)
两式相加可得:2Sn=n-1
∴Sn=
故选C.
点评:本题考查数列求和,考查函数性质,确定f(x)+f(1-x)=1,进而利用倒序相加,是解题的关键.
分析:根据所给函数,确定f(x)+f(1-x)=1,进而利用倒序相加,即可求得结论.
解答:∵f(x)=
 +log2
+log2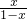 ,
,∴f(1-x)=
 +log2
+log2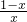 ,
,∴f(x)+f(1-x)=
 +log2
+log2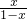 +
+ +log2
+log2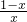 =1
=1∵Sn=f(
 )+f(
)+f( )+…+f(
)+…+f( ),
),∴Sn=f(
 )+f(
)+f(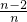 )+…+f(
)+…+f( )
)两式相加可得:2Sn=n-1
∴Sn=

故选C.
点评:本题考查数列求和,考查函数性质,确定f(x)+f(1-x)=1,进而利用倒序相加,是解题的关键.

练习册系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)