题目内容
已知: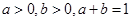 ,(1)求证:
,(1)求证: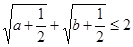
(2)求 的最小值
的最小值
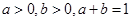 ,(1)求证:
,(1)求证: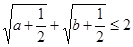
(2)求
 的最小值
的最小值(1)因为 所以
所以 ,所以
,所以
所以 ,从而
,从而 ,所以原不等式成立.
,所以原不等式成立.
(2)8.
 所以
所以 ,所以
,所以
所以
 ,从而
,从而 ,所以原不等式成立.
,所以原不等式成立. (2)8.
试题分析:(1)证明:因为
 所以
所以 ,所以
,所以
所以
 ,从而有2+
,从而有2+
即:

即:
 ,所以原不等式成立.
,所以原不等式成立. (2)
 ……2分
……2分 即
即 当且仅当
当且仅当 时等号成立
时等号成立 即当
即当 时,
时, 的最小值为8.
的最小值为8.点评:在运用基本不等式求最大值和最小值时,要注意“和”或“积”为定值

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 且满足
且满足 ,则
,则 的最小值为
的最小值为 。
。 ,
, 恒成立,则a的取值范围是 .
恒成立,则a的取值范围是 . ,且
,且 ,则
,则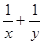 的最小值为
的最小值为  ,若
,若 恒成立,则实数
恒成立,则实数 的最大值为 .
的最大值为 .  、
、 满足
满足 则
则 的最小值为 .
的最小值为 . 满足
满足 ,则
,则 的最大值是____________。
的最大值是____________。
 的图象恒过定点
的图象恒过定点 ,若点
,若点 上,其中
上,其中 ,则
,则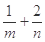 的最小值为 .
的最小值为 .