题目内容
(本小题满分14分)
设函数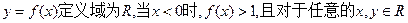 ,有
,有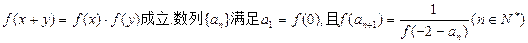 。
。
(1)求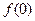 的值;(2)求数列
的值;(2)求数列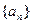 的通项公式;(3)是否存在正数
的通项公式;(3)是否存在正数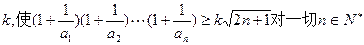 均成立,若存在,求出k的最大值,并证明,否则说明理由。
均成立,若存在,求出k的最大值,并证明,否则说明理由。
设函数
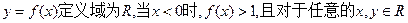 ,有
,有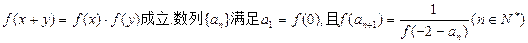 。
。(1)求
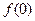 的值;(2)求数列
的值;(2)求数列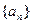 的通项公式;(3)是否存在正数
的通项公式;(3)是否存在正数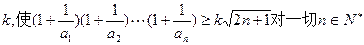 均成立,若存在,求出k的最大值,并证明,否则说明理由。
均成立,若存在,求出k的最大值,并证明,否则说明理由。(1)1
(1)令 --------------3
--------------3
(2)当
设 ,
,


由

 ----------------9
----------------9
(3)存在正数k,使 成立.
成立.
记
∴F(n)单调递增,∴F(1)为F(n)的最小值,由F(n)≥k恒成立知
∴ .--------------------------------14
.--------------------------------14
 --------------3
--------------3(2)当

设
 ,
,


由


 ----------------9
----------------9(3)存在正数k,使
 成立.
成立.记

∴F(n)单调递增,∴F(1)为F(n)的最小值,由F(n)≥k恒成立知

∴
 .--------------------------------14
.--------------------------------14
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
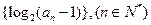 为等差数列,且
为等差数列,且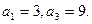 (1)求数列
(1)求数列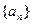 的通项公式;(2)求数列
的通项公式;(2)求数列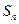
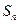 为数列
为数列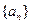 的前
的前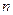 项和,
项和,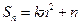 ,
,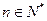 ,其中
,其中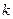 是常数.
是常数.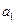 及
及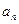 ;
;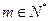 ,
,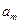 ,
, ,
,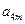 成等比数列,求
成等比数列,求 中,
中,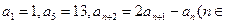 N*),数列
N*),数列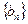 中,
中,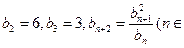 N*),已知点
N*),已知点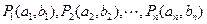
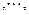 则向量
则向量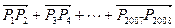 的坐标为( )
的坐标为( )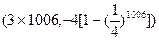
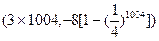
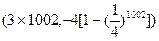
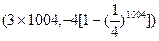
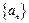 的前
的前 项和为
项和为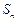 ,且
,且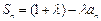 ,其中
,其中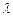 为常数,且
为常数,且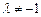 、0.(1)证明:数列
、0.(1)证明:数列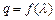 ,数列
,数列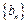 满足
满足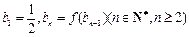 ,求数列
,求数列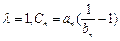 ,数列
,数列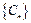 的前
的前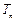 ,求证:当
,求证:当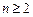 时,
时,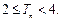
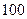 的正整数中,被
的正整数中,被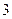 除余
除余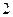 的数的和是 .
的数的和是 . 的前n项和为
的前n项和为 ,若
,若 ,
, ,则该数列的公差d=( )
,则该数列的公差d=( ) 满足
满足 ,且
,且 ,则当
,则当 时,
时,






 中,已知前15项的和
中,已知前15项的和 ,则
,则 等于
等于 B.12 C.
B.12 C. D.6
D.6