题目内容
(10分)已知{an}是公差不为零的等差数列,a1=1,且a1,a3,a9成等比数列.
(1)求数列{an}的通项;
(2)求数列 的前n项和Sn.
的前n项和Sn.
[解] (1)由题设知公差d≠0,
由a1=1,a1,a3,a9成等比数列得:  =
= ,
,
解得d=1或d=0(舍去),
故{an}的通项an=1+(n-1)×1=n.
(2)由(1)知 =2n,
=2n,
由等比数列前n项和公式得:Sn=2+22+23+…+2n= =2n+1-2.
=2n+1-2.

练习册系列答案
相关题目
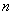 个平面”换成“
个平面”换成“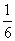 B.
B.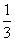 C.
C. D.
D.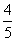
 中,
中, ,则
,则 ( )
( ) 成等比数列,则函数
成等比数列,则函数 的图象与x轴交点的个数是______个.
的图象与x轴交点的个数是______个. ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
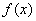 对定义域
对定义域 内的任意
内的任意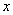 都有
都有 ,且当
,且当 时其导函数
时其导函数 满足
满足 若
若 则( )
则( ) B.
B.
 D.
D.
 的图象,只需将函数
的图象,只需将函数 的图象 ( )
的图象 ( ) 个单位 B.向左平移
个单位 B.向左平移 个单位
个单位  个单位
个单位 ~
~ ,
, ,则
,则 的值是( )
的值是( )