题目内容
(19)在如图所示的几何体中,
(I)求证:![]() ;
;
(II)求![]() 与平面
与平面![]() 所成的角.
所成的角.
本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.
方法一:
(I)证明:因为![]() ,
,![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() .
.
(II)解:过点![]() 作
作![]() 平面
平面![]() ,垂足是
,垂足是![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() .
.

![]() 是直线CM和平面
是直线CM和平面![]() 所成的角.
所成的角.
因为![]() 平面
平面![]() ,
,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以![]() ,
,
则![]() 平面
平面![]() ,因此
,因此![]() .
.
设![]() ,
,![]() ,
,
在直角梯形![]() 中,
中,
![]() ,
,![]() 是
是![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,![]() ,
,
得![]() 是直角三角形,其中
是直角三角形,其中![]() ,
,
所以![]()
在![]() 中,
中,![]() ,
,
所以![]() ,
,
故![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .
.
方法二:
如图,以点![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() 分别为
分别为![]() 轴和
轴和![]() 轴,过点
轴,过点![]() 作与平面
作与平面![]() 垂直的直线为
垂直的直线为![]() 轴,建立直角坐标系
轴,建立直角坐标系![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() .
.

(I)证明:因为![]() ,
,![]() ,
,
所以![]() ,
,
故![]() .
.
(II)解:设向量![]() 与平面
与平面![]() 垂直,则
垂直,则![]() ,
,![]() ,
,
即![]()
因为![]() ,
,![]() ,
,
所以![]() ,z0= -2,
,z0= -2,
即![]() ,
,

直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 是
是![]() 与
与![]() 夹角的余角,
夹角的余角,
所以![]() ,
,
因此直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .
.

练习册系列答案
相关题目
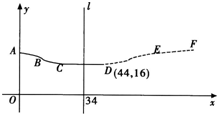 在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票.股民老王在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票.股民老王在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F. .
.
 在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票.股民老王在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票.股民老王在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F. .
. 在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票.股民老王在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA)的变化情况来决定买入或卖出股票.股民老王在研究股票的走势图时,发现一只股票的MA均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老王预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F. .
.