题目内容
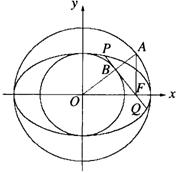
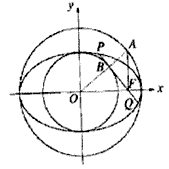
如图,以椭圆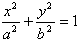 (a>b>0)的中心O为圆心,分别以a和b为半径作大圆和小圆。过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B,设直线BF是小圆的切线,
(a>b>0)的中心O为圆心,分别以a和b为半径作大圆和小圆。过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B,设直线BF是小圆的切线,
(1)证明c2=ab,并求直线BF与y轴的交点M的坐标;
(2)设直线BF交椭圆于P、Q两点,证明
 。
。
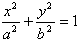 (a>b>0)的中心O为圆心,分别以a和b为半径作大圆和小圆。过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B,设直线BF是小圆的切线,
(a>b>0)的中心O为圆心,分别以a和b为半径作大圆和小圆。过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B,设直线BF是小圆的切线,(1)证明c2=ab,并求直线BF与y轴的交点M的坐标;
(2)设直线BF交椭圆于P、Q两点,证明

 。
。
(1)证明:由题设条件知, ,故
,故 ,
,
即 ,因此
,因此 ; ①
; ①
解:在 中,
中, ,
,
于是,直线OA的斜率 ,
,
设直线BF的斜率为k,则 ,
,
这时,直线BF的方程为 ,
,
令x=0,则 ,
,
所以直线BF与y轴的交点为M(0,a);
(2)证明:由(1),得直线BF的方程为y=kx+a,且 ,②
,②
由已知,设 ,
,
则它们的坐标满足方程组 , ③
, ③
由方程组③消去y,并整理得 ,④
,④
由式①、②和④, ,
,
由方程组③消去x,并整理得 ,⑤
,⑤
由式②和⑤, ;
;
综上,得到 ,
,
注意到 ,
,
得

 。
。
 ,故
,故 ,
,即
 ,因此
,因此 ; ①
; ① 解:在
 中,
中, ,
,于是,直线OA的斜率
 ,
,设直线BF的斜率为k,则
 ,
,这时,直线BF的方程为
 ,
,令x=0,则
 ,
,所以直线BF与y轴的交点为M(0,a);
(2)证明:由(1),得直线BF的方程为y=kx+a,且
 ,②
,②由已知,设
 ,
,则它们的坐标满足方程组
 , ③
, ③ 由方程组③消去y,并整理得
 ,④
,④由式①、②和④,
 ,
,由方程组③消去x,并整理得
 ,⑤
,⑤ 由式②和⑤,
 ;
;综上,得到
 ,
,注意到
 ,
,得


 。
。 
练习册系列答案
相关题目
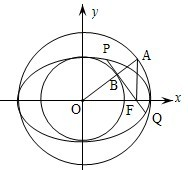 如图,以椭圆
如图,以椭圆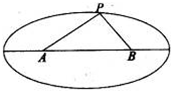 如图,两个工厂A,B(视为两个点)相距2km,现要在以A,B为焦点,长轴长为4km的椭圆上某一点P处建一幢办公楼.据测算此办公楼受工厂A的“噪音影响度”与距离AP成反比,比例系数是1;办公楼受工厂B的“噪音影响度”与距离BP也成反比,比例系数是4.办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP=xkm.
如图,两个工厂A,B(视为两个点)相距2km,现要在以A,B为焦点,长轴长为4km的椭圆上某一点P处建一幢办公楼.据测算此办公楼受工厂A的“噪音影响度”与距离AP成反比,比例系数是1;办公楼受工厂B的“噪音影响度”与距离BP也成反比,比例系数是4.办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP=xkm.