题目内容
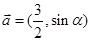 ,
,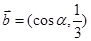 ,且
,且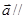
 ,则锐角
,则锐角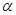 为
为
A. | B.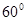 | C. | D.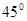 |
D
解析试题分析:根据题意,由于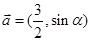 ,
,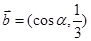 ,且
,且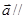
 ,那么则有
,那么则有 ,由于角
,由于角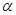 为锐角,那么可知锐角
为锐角,那么可知锐角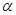 =
=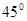 ,故选D.
,故选D.
考点:向量的共线
点评:主要是考查了向量的共线的概念的运用,属于基础题。

 同步练习强化拓展系列答案
同步练习强化拓展系列答案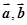 是两个向量,
是两个向量,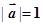 ,
,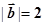 ,且
,且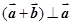 ,则
,则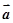 与
与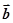 的夹角为( )
的夹角为( )
A.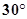 | B. | C.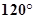 | D.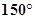 |
若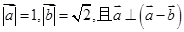 ,则向量
,则向量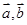 的夹角为
的夹角为
| A.45° | B.60° | C.120° | D.135° |
已知向量 ,
, 满足|
满足| |="2," |
|="2," |  |=l,且(
|=l,且( +
+ )⊥(
)⊥(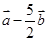 ),则
),则 与
与 的夹角为
的夹角为
A.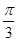 | B.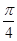 | C.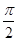 | D.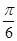 |
已知 ,则
,则
A. | B. | C. | D. |
平面向量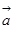 与
与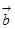 的夹角为
的夹角为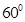 ,
,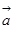 =(2,0),
=(2,0),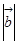 ="1" 则
="1" 则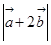 =( )
=( )
A. | B.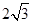 | C.4 | D.12 |
若向量 满足
满足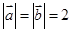 ,且
,且 ,则向量
,则向量 的夹角为
的夹角为
| A.30° | B.45° | C.60° | D.120° |
已知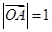 ,
,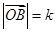 ,
,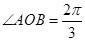 ,点C在
,点C在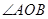 内,
内, 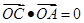 ,若
,若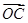 =2m
=2m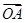 +m
+m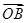 (
(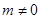 ),则
),则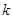 =( )
=( )
| A.1 | B.2 | C.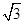 | D.4 |
已知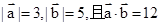 ,则向量
,则向量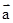 在向量
在向量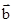 上的投影为( )
上的投影为( )
A.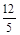 | B.3 | C.4 | D.5 |