题目内容
 如图,折线段AP→PQ→QC是长方形休闲区域ABCD内规划的一条小路,已知AB=1百米,
如图,折线段AP→PQ→QC是长方形休闲区域ABCD内规划的一条小路,已知AB=1百米,
AD=a(a≥1)百米,点P在以A为圆心,AB为半径的圆弧上,PQ⊥BC,Q为垂足.
(1)试问点P在圆弧何处,能使该小路的路程最短?最短路程为多少?
(2)当a=1时,过点P作PM⊥CD,垂足为M.若将矩形PQCM修建为观赏水池,试问点P在圆弧何处,能使水池的面积最大?
解:(1)设∠PAB=α,则 α∈[0, ],PQ=1-cosα,QC=a-sinα,
],PQ=1-cosα,QC=a-sinα,
∴该小路的路程 AP+PQ+QC=1+1-cosα+a-sinα=a+2- sin(α+
sin(α+ ),
),
故当α= 时,AP+PQ+QC 有最小值为 a+2-
时,AP+PQ+QC 有最小值为 a+2- (百米).
(百米).
即点P在圆弧AB的中点时,AP+PQ+QC 有最小值a+2- (百米).
(百米).
(2)当a=1时,矩形矩形PQCM的面积S=PQ•QC=(1-cosα )(1-sinα)=
1-(sinα+cosα)+sinαcosα,设 sinα+cosα=t= sin(
sin( +α)∈[1,
+α)∈[1, ],
],
S=1-t+ =
= (t-1)2 在[1,
(t-1)2 在[1, ]上是单调增函数,∴t=
]上是单调增函数,∴t= 时,即α=
时,即α= 时,
时,
S最大为 -
- ,即点P在圆弧AB的中点时,能使水池的面积最大.
,即点P在圆弧AB的中点时,能使水池的面积最大.
分析:(1)设∠PAB=α,则 α∈[0, ],PQ=1-cosα,QC=a-sinα,该小路的路程 AP+PQ+QC=1+1-cosα+a-sinα=a+2-
],PQ=1-cosα,QC=a-sinα,该小路的路程 AP+PQ+QC=1+1-cosα+a-sinα=a+2- sin(α+
sin(α+ ),可求得AP+PQ+QC 有最小值.
),可求得AP+PQ+QC 有最小值.
(2)当a=1时,矩形矩形PQCM的面积S=PQ•QC=(1-cosα )(1-sinα)=1-(sinα+cosα)+sinαcosα,设 sinα+cosα=t= sin(
sin( +α)∈[1,
+α)∈[1, ],利用S=1-t+
],利用S=1-t+ =
= (t-1)2 在[1,
(t-1)2 在[1, ]上是单调增函数,可求得S的最大值.
]上是单调增函数,可求得S的最大值.
点评:本题考查两角和差的三角函数,以及利用正弦函数的单调性求出式子的最值.
 ],PQ=1-cosα,QC=a-sinα,
],PQ=1-cosα,QC=a-sinα,∴该小路的路程 AP+PQ+QC=1+1-cosα+a-sinα=a+2-
 sin(α+
sin(α+ ),
),故当α=
 时,AP+PQ+QC 有最小值为 a+2-
时,AP+PQ+QC 有最小值为 a+2- (百米).
(百米).即点P在圆弧AB的中点时,AP+PQ+QC 有最小值a+2-
 (百米).
(百米).(2)当a=1时,矩形矩形PQCM的面积S=PQ•QC=(1-cosα )(1-sinα)=
1-(sinα+cosα)+sinαcosα,设 sinα+cosα=t=
 sin(
sin( +α)∈[1,
+α)∈[1, ],
],S=1-t+
 =
= (t-1)2 在[1,
(t-1)2 在[1, ]上是单调增函数,∴t=
]上是单调增函数,∴t= 时,即α=
时,即α= 时,
时,S最大为
 -
- ,即点P在圆弧AB的中点时,能使水池的面积最大.
,即点P在圆弧AB的中点时,能使水池的面积最大.分析:(1)设∠PAB=α,则 α∈[0,
 ],PQ=1-cosα,QC=a-sinα,该小路的路程 AP+PQ+QC=1+1-cosα+a-sinα=a+2-
],PQ=1-cosα,QC=a-sinα,该小路的路程 AP+PQ+QC=1+1-cosα+a-sinα=a+2- sin(α+
sin(α+ ),可求得AP+PQ+QC 有最小值.
),可求得AP+PQ+QC 有最小值.(2)当a=1时,矩形矩形PQCM的面积S=PQ•QC=(1-cosα )(1-sinα)=1-(sinα+cosα)+sinαcosα,设 sinα+cosα=t=
 sin(
sin( +α)∈[1,
+α)∈[1, ],利用S=1-t+
],利用S=1-t+ =
= (t-1)2 在[1,
(t-1)2 在[1, ]上是单调增函数,可求得S的最大值.
]上是单调增函数,可求得S的最大值.点评:本题考查两角和差的三角函数,以及利用正弦函数的单调性求出式子的最值.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
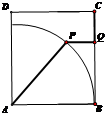 如图,折线段AP→PQ→QC是长方形休闲区域ABCD内规划的一条小路,已知AB=1百米,
如图,折线段AP→PQ→QC是长方形休闲区域ABCD内规划的一条小路,已知AB=1百米, (2012•上高县模拟)如图,等腰△ABC的底边AB=6,高CD=3,点E是线段BD上异于点B、D的动点,点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACFE的体积.
(2012•上高县模拟)如图,等腰△ABC的底边AB=6,高CD=3,点E是线段BD上异于点B、D的动点,点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACFE的体积.
