题目内容
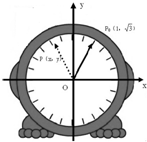如图，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒尖位置P（x，y），其初始位置为P0（1，| 3 |
y=2sin（-
t+
）
| π |
| 30 |
| π |
| 3 |
y=2sin（-
t+
）
．| π |
| 30 |
| π |
| 3 |
分析：求出转速ω 的值，再求出经过时间t，秒针与x正半轴的夹角以及秒针的长度为|OP|，即可求得点P的纵坐标y与时间t的函数关系．
解答：解：由于秒针每60秒顺时针转一周，故转速ω=-
=-
，
由于初始位置为P0（1，
），故经过时间t，秒针与x正半轴的夹角为-
t+
，
再由秒针的长度为|OP|=2，可得点P的纵坐标y与时间t的函数关系为y=2sin（-
t+
），
故答案为 y=2sin（-
t+
）．
| 2π |
| 60 |
| π |
| 30 |
由于初始位置为P0（1，
| 3 |
| π |
| 30 |
| π |
| 3 |
再由秒针的长度为|OP|=2，可得点P的纵坐标y与时间t的函数关系为y=2sin（-
| π |
| 30 |
| π |
| 3 |
故答案为 y=2sin（-
| π |
| 30 |
| π |
| 3 |
点评：本题主要考查由函数y=Asin（ωx+∅）的部分图象求函数的解析式，属于中档题．
练习册系列答案
相关题目
如图，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位置p（x，y）．若初始位置为P0（
，
），当秒针从P （注此时t=0）正常开始走时，那么点P的纵坐标y与时间t的函数关系为（ ）
）
）
）
，
），当秒针从P （注此时t=0）正常开始走时，那么点P的纵坐标y与时间t的函数关系为（ ）
）
）
）
），当秒针从P0（注此时t=0）正常开始走时，那么点P的纵坐标y与时间t的函数关系为 ﹡ ．