题目内容
设过点P(-2,4),倾斜角为
π的直线l与抛物线C相交于A、B两点，抛物线C的顶点在原点，以x轴为对称轴，若|PA|、|AB|、|PB|成等比数列，求抛物线C的方程.
思路解析：关键是|PA|、|AB|、|PB|成等比数列条件的运用，因为P、A、B都在直线l上，所以可转化为它们对应纵坐标之间的关系，找到关于系数的方程，求得系数即可. 解：由题意，直线l的方程为y=-x+2，设C的方程为y2=2ax（a≠0），由 ∴|y1y2-4(y1+y2)+16|=(y1+y2)2-4y1y2，且y1≠y2. ∴|a+4|=a2+4a，且Δ=4a2+16a＞0, 解得a=1，即C的方程为y2=2x.
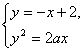消去x，得y2+2ay-4a=0，设A、B纵坐标分别为y1、y2，则y1+y2=-2a，y1·y2=-4a，∵P、A、B共线且|PA|、|AB|、|PB|成等比数列，则|y1-4|、|y1-y2|、|y2-4|也成等比数列，∴|y1-4|·|y2-4|=|y1-y2|2≠0.
练习册系列答案
巴蜀英才课课练与单元测试系列答案
听力特训营系列答案
智慧万羽中考试题荟萃系列答案
新课标三维同步训练系列答案
同步练习册课时练系列答案
名师精选卷系列答案
孟建平专题突破系列答案
方洲新概念名师手把手系列答案
相关题目