题目内容
若三棱柱ABC-A'B'C'的体积是12，则四棱锥C'-A'B'BA的体积是
8
8
．分析：因为棱锥C'-ABC与棱柱同底同高，由Sh=12，知棱锥C'-ABC与的体积V=
Sh=4，由此能求出四棱锥C'-A'B'BA的体积．
| 1 |
| 3 |
解答：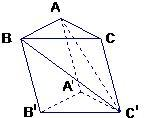
解：因为棱锥C'-ABC与棱柱同底同高，
∵Sh=12，
∴棱锥C'-ABC的体积V=
Sh=4．
故四棱锥C'-A'B'BA的体积=12-4=8．
故答案为：8．
解：因为棱锥C'-ABC与棱柱同底同高，∵Sh=12，
∴棱锥C'-ABC的体积V=
| 1 |
| 3 |
故四棱锥C'-A'B'BA的体积=12-4=8．
故答案为：8．
点评：本题考查棱柱、棱锥的体积的运算，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
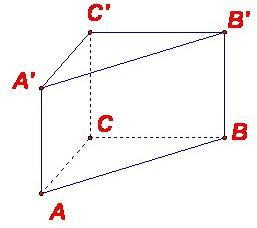如图，在直三棱柱ABC-A′B′C′中，CC′=AC=BC=2，∠ACB=90°．
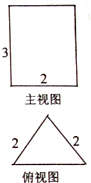若三棱柱ABC-A1B1C1的主视图、俯视图及其相应尺寸如图所示，则该三棱柱的左视图的面积为（ ）
如图，在正三棱柱ABC-A'B'C'中，AB=2，若二面角C'-AB-C的大小为60°，则点C到平面ABC'的距离为