Question

在平面直角坐标系中,点P沿x轴正方向,点Q沿y轴正方向,点R沿斜率为1的直线向上分别以一定的速度a、b、c运动,且P、Q、R恒在一条直线上,在某一时刻P、Q、R的位置分别为(4,0)、(0,2)、(2,1),试探讨:当点P、Q、R运动时,a、b、c的比值是否为定值?并加以说明.

Answer 1

思路解析：本题考查对直线方程、直线的斜率的理解,及直线的图形的应用,本题要理解在运动过程中各点位置的变化情况.

解：设P₀(4,0)、Q₀(0,2)、R₀(2,1)且将P、Q、R分别看作由P₀、Q₀、R₀同时出发,分别沿x轴正方向,y轴正方向,斜率为1的直线向上方向匀速运动,经过时间t后(t＞0),它们的坐标为P(4+at,0)、Q(0,2+bt)、R(2+,1+),则PQ的方程为=1.

∵P、Q、R恒在一条直线上,将R代入上式,即［bc+ac-ab］t²+［bc-(a+2b)］t=0对一切t＞0恒成立.

∴

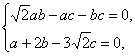
消去c得a²-3ab+2b²=0.

得a=b或a=2b.

当a=b时,c=b,此时a∶b∶c=2∶2∶;

当a=2b时,c=b,此时a∶b∶c=6∶3∶2.