题目内容
已知a，b，c为任意实数，且a＞b，则下列不等式中恒成立的是（ ）
| A、ac＞bc | ||||
| B、a+c＞b+c | ||||
| C、ac2＞bc2 | ||||
D、
|
考点：不等式的基本性质
专题：不等式的解法及应用
分析：由条件a＞b，利用不等式的性质可得a+c＞b+c，从而得出结论．
解答：
解：∵a，b，c为任意实数，且a＞b，∴由不等式的性质可得 a+c＞b+c，
故选：B．
故选：B．
点评：本题主要考查不等式的基本性质，属于基础题．
练习册系列答案
相关题目
中国古代数学著作《九章算法》中的“更相减损术”可用来求两个正整数的最大公约数．现应用此法求168与93的最大公约数：记（168，93）为初始状态，则第一步可得（75，93），第二步得到（75，18），…．以上解法中，不会出现的状态是（ ）
| A、（57，18） |
| B、（3，18） |
| C、（6，9） |
| D、（3，3） |
在20瓶饮料中，有4瓶已过了保质期．从这20瓶饮料中任取1瓶，取到已过保质期饮料的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
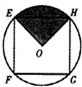如图，EFGH是以O为圆心，1为半径的圆的内接正方形，将一颗豆子随机地掷到圆内，用A表示事件“豆子落在正方形EFGH内”，B表示事件“豆子落在扇形HOE（阴影部分）内”，则P（B|A）=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
观察数列；-4，0，4，1，-4，0，4，1，-4，0，4，1…，则a2014=（ ）
| A、-4 | B、0 | C、4 | D、1 |
已知命题p：?x0＞0，lnx0＜0．则￢p为（ ）
| A、?x＞0，lnx≥0 |
| B、?x≤0，lnx≥0 |
| C、?x0＞0，lnx0≥0 |
| D、?x0≤0，lnx0＜0 |
对于等式：cos4x=cos3x+cosx，下列说法正确的是（ ）
| A、对于任意x∈R，等式都成立 |
| B、对于任意x∈R，等式都不成立 |
| C、存在无穷多个x∈R使等式成立 |
| D、等式只对有限多个x∈R成立 |
计算sin（-960°）的值为（ ）
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|