题目内容
若非零向量
,
满足|
|=|
|=|
-
|,则
与
+
的夹角为
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
30°
30°
.分析:设
=
,
=
,以
、
为邻边作平行四边形,根据平行四边形法则,可得
-
=
与
+
=
,进而根据题意,分析可得四边形OACB为菱形,且∠BOA=60°,由菱形的性质,易得∠AOC的大小,由向量夹角的定义,可得
与
+
的夹角就是∠AOC,即可得答案.
| OA |
| a |
| OB |
| b |
| OA |
| OB |
| a |
| b |
| BA |
| a |
| b |
| OC |
| a |
| a |
| b |
解答: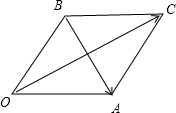 解:作
解:作
=
,
=
,以
、
为邻边作平行四边形,如图:
则
-
=
-
=
,
+
=
,
由|
|=|
|,可得平行四边形OACB为菱形,则OC为∠BOA的角平分线,
根据题意,|
|=|
|=|
-
|,即
=
=
,则∠BOA=60°,
又由OC为∠BOA的角平分线,则∠AOC=30°,
与
+
的夹角就是∠AOC,则
与
+
的夹角为30°;
故答案为30°
 解:作
解:作| OA |
| a |
| OB |
| b |
| OA |
| OB |
则
| a |
| b |
| OA |
| OB |
| BA |
| a |
| b |
| OC |
由|
| a |
| b |
根据题意,|
| a |
| b |
| a |
| b |
| OA |
| OB |
| BA |
又由OC为∠BOA的角平分线,则∠AOC=30°,
| a |
| a |
| b |
| a |
| a |
| b |
故答案为30°
点评:本题考查平行四边形法则的运用,涉及夹角问题,注意向量的夹角与几何角的区别与联系,本题也可以用数量积来解答.

练习册系列答案
相关题目
下列命题中假命题 是( )
A、若|
| ||||||||||||||||
B、
| ||||||||||||||||
C、若△ABC中,a=5,b=8,c=7,则
| ||||||||||||||||
D、若非零向量
|