题目内容
已知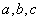 是正数,
是正数, 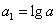 ,
,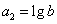 ,
,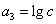 .
.
(Ⅰ)若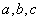 成等差数列,比较
成等差数列,比较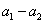 与
与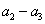 的大小;
的大小;
(Ⅱ)若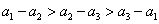 ,则
,则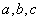 三个数中,哪个数最大,请说明理由;
三个数中,哪个数最大,请说明理由;
(Ⅲ)若 ,
,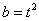 ,
,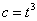 (
(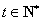 ),且
),且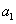 ,
,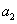 ,
,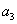 的整数部分分别是
的整数部分分别是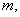

 求所有
求所有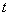 的值.
的值.
解:(Ⅰ)由已知得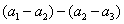 =
=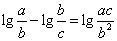 .
.
因为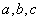 成等差数列,所以
成等差数列,所以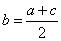 ,
,
则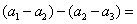
 ,
,
因为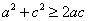 ,所以
,所以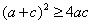 ,即
,即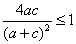 ,
,
则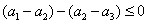 ,即
,即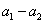

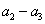 ,当且仅当
,当且仅当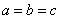 时等号成立.
时等号成立.
……………… 4分
(Ⅱ)解法1:令 ,
,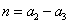 ,
,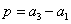 ,
,
依题意,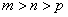 且
且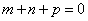 ,所以
,所以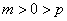 .
.
故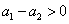 ,即
,即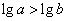 ;且
;且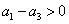 ,即
,即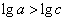 .
.
所以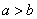 且
且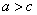 .
.
故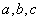 三个数中,
三个数中,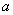 最大.
最大.
解法2:依题意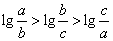 ,即
,即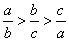 .
.
因为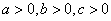 ,所以
,所以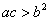 ,
,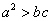 ,
,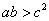 .
.
于是,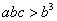 ,
,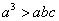 ,
,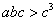 ,
,
所以 ,
,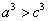 .
.
因为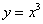 在
在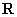 上为增函数,所以
上为增函数,所以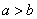 且
且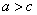 .
.
故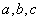 三个数中,
三个数中,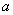 最大. ……………… 8分
最大. ……………… 8分
(Ⅲ)依题意,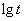 ,
,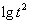 ,
,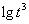 的整数部分分别是
的整数部分分别是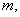

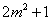 ,则
,则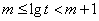 ,
,
所以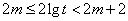 .
.
又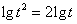 ,则
,则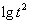 的整数部分是
的整数部分是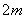 或
或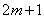 .
.
当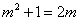 时,
时,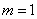 ;
;
当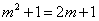 时,
时,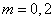 .
.
当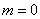 时,
时,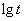 ,
,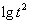 ,
,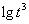 的整数部分分别是
的整数部分分别是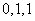 ,
,
所以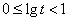 ,
,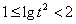 ,
,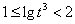 .所以
.所以 ,解得
,解得 .
.
又因为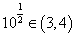 ,
,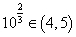 ,所以此时
,所以此时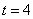 .
.
(2)当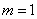 时,同理可得
时,同理可得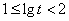 ,
,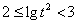 ,
,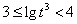 .
.
所以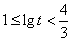 ,解得
,解得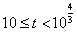 .又
.又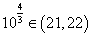 ,此时
,此时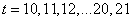 .
.
(3)当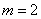 时,同理可得
时,同理可得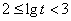 ,
,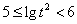 ,
,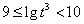 ,
,
同时满足条件的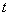 不存在.
不存在.
综上所述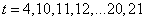 .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 ,若
,若 ,则
,则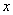 的值为 .
的值为 .  中,
中, ,
, ,
, ,则
,则 ______;△
______;△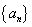 满足
满足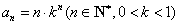 下面说法正确的是
下面说法正确的是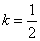 时,数列
时,数列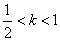 时,数列
时,数列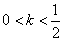 时,数列
时,数列 为正整数时,数列
为正整数时,数列 .
. 的最小值;
的最小值; ,求
,求 的值.
的值. (A)9
(A)9 (B)10
(B)10
 与圆
与圆 相交于
相交于 、
、 两点,且
两点,且 ,则
,则 .
. (其中
(其中 、
、 为有理数),则
为有理数),则 .
.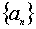 ,满足
,满足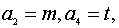 且
且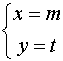 是增广矩阵
是增广矩阵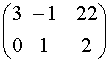 的线性方程组
的线性方程组 的解,则无穷等比数列
的解,则无穷等比数列