题目内容
已知O为原点,若点A、B的坐标分别为(a,0)、(0,a),a∈R+,当点P在线段AB上,且 ,(0≤t≤1),则
,(0≤t≤1),则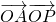 的最大值是
的最大值是
- A.a
- B.2a2
- C.a2
- D.3a
C
分析:由 =(-ta,ta)(0≤t≤1),可求P,代入
=(-ta,ta)(0≤t≤1),可求P,代入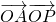 ,整理结合t得范围可求最大值
,整理结合t得范围可求最大值
解答:∵A、B的坐标分别为(a,0)、(0,a),则
∵ =(-ta,ta)(0≤t≤1),设P(x,y)
=(-ta,ta)(0≤t≤1),设P(x,y)
∴ 即P(a-at,at)
即P(a-at,at)
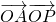 =(a,0)•(a-at,at)=a2(1-t)≤a2
=(a,0)•(a-at,at)=a2(1-t)≤a2
即所求的最大值为a2
故选C
点评:本题主要考查了向量的基本运算及向量共线的坐标表示,属于基础试题
分析:由
 =(-ta,ta)(0≤t≤1),可求P,代入
=(-ta,ta)(0≤t≤1),可求P,代入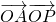 ,整理结合t得范围可求最大值
,整理结合t得范围可求最大值解答:∵A、B的坐标分别为(a,0)、(0,a),则

∵
 =(-ta,ta)(0≤t≤1),设P(x,y)
=(-ta,ta)(0≤t≤1),设P(x,y)∴
 即P(a-at,at)
即P(a-at,at)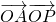 =(a,0)•(a-at,at)=a2(1-t)≤a2
=(a,0)•(a-at,at)=a2(1-t)≤a2即所求的最大值为a2
故选C
点评:本题主要考查了向量的基本运算及向量共线的坐标表示,属于基础试题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,(0≤t≤1),则
,(0≤t≤1),则 的最大值是( )
的最大值是( ) ,(0≤t≤1),则
,(0≤t≤1),则 的最大值是( )
的最大值是( ) ,(0≤t≤1),则
,(0≤t≤1),则 的最大值是( )
的最大值是( )