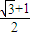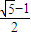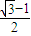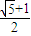题目内容
已知点F,A分别是椭圆
+
=1 (a>b>0)的左焦点、右顶点,B(0,b)满足
•
=0,则椭圆的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| FB |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:首先根据
•
=0推断出FB⊥AB,进而根据勾股定理可知|FB|2+|AB|2=(a+c)2,把进而整理关于a和c的方程求得
即离心率e的值.
| FB |
| AB |
| c |
| a |
解答:解解:∵
•
=0
∴FB⊥AB
∴|FB|2+|AB|2=(a+c)2,即b2+c2+a2+b2=(a+c)2,整理得2ac-2b2=0即ac=a2-c2
等号两边同时除以a2得
+
-1=0,即e2+e-1=0
求得e=
∵e>0
∴e=
故选B
| FB |
| AB |
∴FB⊥AB
∴|FB|2+|AB|2=(a+c)2,即b2+c2+a2+b2=(a+c)2,整理得2ac-2b2=0即ac=a2-c2
等号两边同时除以a2得
| c2 |
| a2 |
| c |
| a |
求得e=
-1±
| ||
| 2 |
∵e>0
∴e=
-1+
| ||
| 2 |
故选B
点评:本题主要考查了椭圆的简单性质.要求学生熟练掌握椭圆的标准方程中a,b和c的关系以及椭圆的图象.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
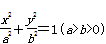 的左焦点、右顶点,B(0,b)满足
的左焦点、右顶点,B(0,b)满足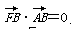 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )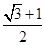 B.
B.  C.
C. 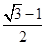 D.
D. 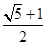
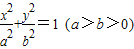 的左焦点、右顶点,B(0,b)满足
的左焦点、右顶点,B(0,b)满足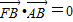 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )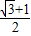

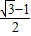

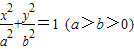 的左焦点、右顶点,B(0,b)满足
的左焦点、右顶点,B(0,b)满足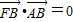 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )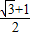
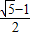
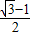
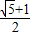
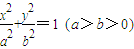 的左焦点、右顶点,B(0,b)满足
的左焦点、右顶点,B(0,b)满足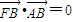 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )