题目内容
(本小题14分)已知函数 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当 ≤0时,
≤0时,
 .
.

(1)求出 的解析式;
的解析式;
(2)现已画出函数 在y轴左侧的图像,如图所示,请补出完整函数
在y轴左侧的图像,如图所示,请补出完整函数 的图像,并根据图像写出函数
的图像,并根据图像写出函数 的增区间和值域。
的增区间和值域。
(1) ;(2)单调增区间为:
;(2)单调增区间为: 和
和 ;值域为:
;值域为: .
.
【解析】
试题分析:(1)当 时,
时, ,又函数为偶函数所以
,又函数为偶函数所以 ,最后写成分段函数的形式
,最后写成分段函数的形式 ;(2)找出已画出函数
;(2)找出已画出函数 在y轴左侧的图像的几个特殊对称点,然后用一条光滑的曲线将其连接起来,即可得到
在y轴左侧的图像的几个特殊对称点,然后用一条光滑的曲线将其连接起来,即可得到 在y轴右侧的图像,从图像上可看出函数的单调区间,从图像上可分析出
在y轴右侧的图像,从图像上可看出函数的单调区间,从图像上可分析出
试题解析:(1)当 时,
时, ,又函数为偶函数所以
,又函数为偶函数所以 ,所以
,所以 ;
;
(2)
从图像可分析出单调增区间为: 和
和 ;当
;当 时,
时, 值域为:
值域为: .
.
考点:1、函数的奇偶性;2、函数的单调性;3、函数的值域.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 的前
的前 项和
项和 当首项
当首项 和公差
和公差 变化时,若
变化时,若 是一个定值,则下列各数中为定值的是( )
是一个定值,则下列各数中为定值的是( )  B.
B. C.
C. D.
D.
 中,
中, 分别是角
分别是角 的对边,且满足
的对边,且满足 ,那么
,那么 (
( )为奇函数,
)为奇函数, ,
, ,则
,则
 D.5
D.5 的解集为
的解集为 ,则
,则 .
. 的值域是( )
的值域是( )  B.
B. C.
C.  D.
D. 
 ,
, 分别是R上的奇函数,偶函数,且满足
分别是R上的奇函数,偶函数,且满足 ,则有
,则有 B.
B.
 D.
D.
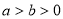 ,椭圆
,椭圆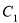 的方程为
的方程为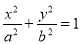 ,双曲线
,双曲线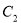 的方程为
的方程为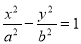 ,
,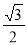 ,则
,则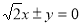 B.
B.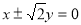 C.
C.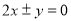 D.
D.